XC4008E-1PG191C交流等效电路
发布时间:2019/11/12 17:46:32 访问次数:947
XC4008E-1PG191C值得指出的是,LC选频放大电路是构成lC正弦波振荡器的基础。由于调谐回路的选频作用,它不仅可工作在甲类,而且还可工作在乙类或丙类。LC并联谐振电路o值高,选频性能好,即使电流有失真、输出电压也基本为正弦形。
选频放大电路的幅频响应具有与图9.7.2a类似的曲线。变压器反馈式LC振荡电路.
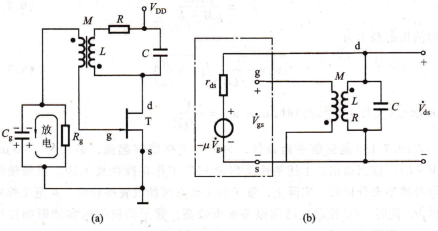
电路的组成及起振条件图9,7.4a是采用JFET的变压器反馈式LC振荡电路。图中LC并联谐振回路作为管子的漏极负载,与乙串联的电阻R表示回路的等效损耗。反馈信号通过一变压器二次线圈传送到栅极回路,Rg′cg是用来产生栅偏压的.在
谐振频率ω=ω0≈1/・√LC的情况下,LC回路呈纯电阻性质,并且数值最大[|z|=L/(RC)],这样,JFET的漏极输出电压与栅极输入电压将产生180°的相位移,即♀a=180°,同时根据图中标出的变压器的同名端符号“・”,二次线圈又引人了180°的相位移(设变压器二次侧的负载电阻很大),即田f=180°,这样,整个闭合环路的相位移为♀a+♀f=180°+180°=360°,满足了相位平衡条件。但相位条件满足了,只说明电路有可能产生自激振荡,还不一定就能产生振荡。为了确保电路能振荡,还必须满足振幅条件。为此,要求对电路进行分析,以得出放大器件的参数与电路参数之间的确定关系。它的交流等效电路模型如图9.7.4b所示。考虑到场效应管的电压放大系数u=gm rds,则由图可知,放大电路的电压增益为
AV=-UZ/Z+RDE=-U/1+RDE/Z
考虑到并联谐振回路的导纳为
1/=1/R+JWL+jωc=1+(-W2)LC+JWCR/R+JWL
因而上式可以改写为
AV=-U/1+RDE/Z=1+(-W2)LC=JWCR/-R+rds[1 +(-ω2)LC] +jω(L+CRrds) (9.7.10)
反馈系数
FV=VGS/VDS
式中yds/(R+jωL)为并联谐振回路中通过电感的电流。
所以
FV=-JWM/R+JWL
由式(9.7.10)及式(9,7.11)得
GM=vRC=UM-L
根据振荡平衡条件AvFv,此时的振荡频率为
R+rds(1 -ω2LC) +jD(L+CRrds)=1,令式(9.7.12)等于1,得此RC=zjωuM
当R<<r 实际上是如此)时ω=ωO=1/LC
式(⒐7,13)是振幅平衡条件,为了使电路能够起振,必须使gm)uRc/(uM-L)。应当指出,上述条件是假设FET工作在线性放大区,用低频时的小信号模型来分析的。实际上,管子的工作点可能设置得较低,甚至工作到截止区①,同时,乙C振荡电路的振荡频率较高,管子的极间电容的影响往往不能忽略,因而式(9,7.13)和式(9,7.14)是近似的。
振荡的建立和稳定,图9.7,4所示电路的栅偏压是由Rg′cg所产生的。在建立振荡的过程中,它们的栅源极间起整流元件的作用,栅极为正极,源极为负极,Rg′cg为整流电路的负载,Cg起滤波作用①。当时间常数tg=Rg Cg大于振荡信号的周期时,电容Cg将被充电到接近栅极信号电压的峰值,此电压就是电路的栅偏压VG。
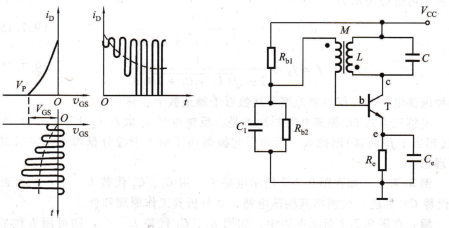
当电源yDD接通后,由于电路中存在噪声或某种扰动,经过放大与选频循环往复,振荡就逐步建立起来。开始时,由于栅偏压ycs=0,管子的跨导gm较大,此时,|AI Fr|>1,易于起振,随着振幅的不断增长,栅偏压|ycs|增加(更负),管子的工作点下移,gm值减小,直至|AvFv|=1,振荡趋于稳定,这样,自偏压环节和管子的非线性能够自动地调整输出幅度。结合前面的讨论,式(9.7.13)所给出的gm值可以理解为确定振幅的平均跨导值,为了使电路易于起振,实际的gm值应比此式所确定的值为大。图9.7.5画出了在起振过程中栅极电压和漏极电流的波形图,由图可知,漏极电流JD为非正弦形,但是由于漏极负载是LC并联谐振回路,选择性较强,所以输出波形还是正弦波(用第三个线圈耦合输出,图中未画出),这种工作状态是不同于RC振荡电路的,在后一种电路中,放大器件是工作于线性放大区。
图9,7,6所示是用BJT组成的变压器反馈式乙C振荡电路。Rbl、RE、Rb2稳定管子的静态工作点,Ce和C1均为交流旁路电容。选用B较大的管子(例如B≥50)或增加变压器一次侧和二次侧之间的耦合程度(增加互感M),或增加二次线圈的匝数,都可使电路易于起振。
深圳市唯有度科技有限公司http://wydkj.51dzw.com/
XC4008E-1PG191C值得指出的是,LC选频放大电路是构成lC正弦波振荡器的基础。由于调谐回路的选频作用,它不仅可工作在甲类,而且还可工作在乙类或丙类。LC并联谐振电路o值高,选频性能好,即使电流有失真、输出电压也基本为正弦形。
选频放大电路的幅频响应具有与图9.7.2a类似的曲线。变压器反馈式LC振荡电路.
电路的组成及起振条件图9,7.4a是采用JFET的变压器反馈式LC振荡电路。图中LC并联谐振回路作为管子的漏极负载,与乙串联的电阻R表示回路的等效损耗。反馈信号通过一变压器二次线圈传送到栅极回路,Rg′cg是用来产生栅偏压的.在
谐振频率ω=ω0≈1/・√LC的情况下,LC回路呈纯电阻性质,并且数值最大[|z|=L/(RC)],这样,JFET的漏极输出电压与栅极输入电压将产生180°的相位移,即♀a=180°,同时根据图中标出的变压器的同名端符号“・”,二次线圈又引人了180°的相位移(设变压器二次侧的负载电阻很大),即田f=180°,这样,整个闭合环路的相位移为♀a+♀f=180°+180°=360°,满足了相位平衡条件。但相位条件满足了,只说明电路有可能产生自激振荡,还不一定就能产生振荡。为了确保电路能振荡,还必须满足振幅条件。为此,要求对电路进行分析,以得出放大器件的参数与电路参数之间的确定关系。它的交流等效电路模型如图9.7.4b所示。考虑到场效应管的电压放大系数u=gm rds,则由图可知,放大电路的电压增益为
AV=-UZ/Z+RDE=-U/1+RDE/Z

考虑到并联谐振回路的导纳为
1/=1/R+JWL+jωc=1+(-W2)LC+JWCR/R+JWL
因而上式可以改写为
AV=-U/1+RDE/Z=1+(-W2)LC=JWCR/-R+rds[1 +(-ω2)LC] +jω(L+CRrds) (9.7.10)
反馈系数
FV=VGS/VDS
式中yds/(R+jωL)为并联谐振回路中通过电感的电流。
所以
FV=-JWM/R+JWL
由式(9.7.10)及式(9,7.11)得
GM=vRC=UM-L
根据振荡平衡条件AvFv,此时的振荡频率为
R+rds(1 -ω2LC) +jD(L+CRrds)=1,令式(9.7.12)等于1,得此RC=zjωuM
当R<<r 实际上是如此)时ω=ωO=1/LC
式(⒐7,13)是振幅平衡条件,为了使电路能够起振,必须使gm)uRc/(uM-L)。应当指出,上述条件是假设FET工作在线性放大区,用低频时的小信号模型来分析的。实际上,管子的工作点可能设置得较低,甚至工作到截止区①,同时,乙C振荡电路的振荡频率较高,管子的极间电容的影响往往不能忽略,因而式(9,7.13)和式(9,7.14)是近似的。
振荡的建立和稳定,图9.7,4所示电路的栅偏压是由Rg′cg所产生的。在建立振荡的过程中,它们的栅源极间起整流元件的作用,栅极为正极,源极为负极,Rg′cg为整流电路的负载,Cg起滤波作用①。当时间常数tg=Rg Cg大于振荡信号的周期时,电容Cg将被充电到接近栅极信号电压的峰值,此电压就是电路的栅偏压VG。
当电源yDD接通后,由于电路中存在噪声或某种扰动,经过放大与选频循环往复,振荡就逐步建立起来。开始时,由于栅偏压ycs=0,管子的跨导gm较大,此时,|AI Fr|>1,易于起振,随着振幅的不断增长,栅偏压|ycs|增加(更负),管子的工作点下移,gm值减小,直至|AvFv|=1,振荡趋于稳定,这样,自偏压环节和管子的非线性能够自动地调整输出幅度。结合前面的讨论,式(9.7.13)所给出的gm值可以理解为确定振幅的平均跨导值,为了使电路易于起振,实际的gm值应比此式所确定的值为大。图9.7.5画出了在起振过程中栅极电压和漏极电流的波形图,由图可知,漏极电流JD为非正弦形,但是由于漏极负载是LC并联谐振回路,选择性较强,所以输出波形还是正弦波(用第三个线圈耦合输出,图中未画出),这种工作状态是不同于RC振荡电路的,在后一种电路中,放大器件是工作于线性放大区。
图9,7,6所示是用BJT组成的变压器反馈式乙C振荡电路。Rbl、RE、Rb2稳定管子的静态工作点,Ce和C1均为交流旁路电容。选用B较大的管子(例如B≥50)或增加变压器一次侧和二次侧之间的耦合程度(增加互感M),或增加二次线圈的匝数,都可使电路易于起振。

深圳市唯有度科技有限公司http://wydkj.51dzw.com/


 公网安备44030402000607
公网安备44030402000607





