W58-XB1A4A-4导磁体内总会有磁阻
发布时间:2019/10/28 12:07:56 访问次数:612
W58-XB1A4A-4式中,Φδ的单位为Mx。
值得指出的是,麦克斯韦吸力公式和由能量守恒定律计算出来的吸力公式是可以互相转换的。但是麦克斯韦吸力公式适合于磁极间磁场均匀分布的情况。由于铁磁材料的导磁系数远比空气大得多,只要未达到饱和,磁力线可以认为是垂直于磁极表面的;而当气隙不大时,其分布又往往是比较均匀的。因此,用麦克斯韦公式可更方便地计算吸力,并且具有一定的精确度。
典型直流电磁铁的吸力特性,拍合式电磁铁的吸力特性,假如拍合式电磁铁吸片转动时,由于吸片转角α和气隙a一般都很小,为了大致看看吸力特性的变化规律,可以近似认为气隙磁导^δ=号气而代入式(1-10)得
另外,还可以忽略铁磁阻和非工作气隙的磁阻,则σ斋δ就近似等于线圈磁势rW而且不随气隙a的变化而变化。因此式(1-26)就可表为
Fd=c(rw)2 (N) (1~27)
式,(1-27)中设C=σ7)2踟S为常数,即不随气隙a而变化,那么有这是二次双曲线函数的关系,如图1-18中虚线1所示。
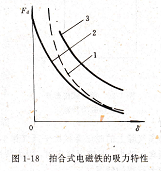
实际上,导磁体内总会有磁阻,所以tr缶δ不等于刀巳而是随a的减小而减小,因为ε减小时,磁通增大,导磁体内磁压降就会增大◇因此,实际的吸力特性偏离双曲线,a越小,导磁体的磁压降就越大,曲线偏离也越大,如图1-18中曲线2所示。 拍合式电磁铁的吸力特性,若忽略铁磁阻而假定饥nδccr″,则在某一气隙下,Fd∝σ″)2,即当磁势增大时,吸力特性上移,如图中曲线3所示。由于二次双曲线函数很陡,也就是说,拍合式电磁铁的吸力将随着气隙增大而减小很多,所以这种电磁铁不宜用于行程要求较大的情况。
E型拍合式电磁铁(图1-2(b))的吸力特性要比U型的更陡,即在闭合位置时,E型
的吸力比U型大得多,但在打开位置时,大得就不显著了。对于衔铁位于侧面的拍合式电磁铁(图1-3),其漏磁通通过吸片,因此还应该考虑漏磁通产生的力矩M洳,即Md=Mdδ+1f,式中Mdδ为主工作气隙磁通所产生的力矩。
吸入式电磁铁的吸力特性由前面分析可知,吸入式电磁铁的吸力计算公式为式(1-17)所表示。对于吸入式电磁铁的吸力特性有以下几个特点:
若铁心为平顶,则当ε不是很大时可以
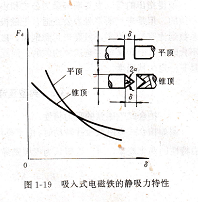
认为^δ=u。苄(S为极面面积),而话等=Qa2,因此,Fdδ=r(a)的特性同拍合式相近,即随a的增大,Fdδ减小很多。但是,当a变化时,漏磁通Φσ1却改变不多(因为a的变化量相对Ja来说是不大的),所以Fdσ不会因a的增大而减小很多。这就使得吸入式电磁铁的吸力要比拍合式的大,并且,在打开位置时,螺管力 图1-19 吸人式电磁铁的静吸力特性所占的比例更大。因此,它适用于需要铁心行程较大的情况。
螺管力Fdc与线圈磁势σ″)2成正比,因此,增大IⅥ/就可以增大Fdσ・而不会受磁路饱和所限,这就使吸入式电磁铁适用于短时产生较大的吸力,因为线圈短时通以很大电流并不会发热过甚。而拍合式电磁铁没有这一特点,因为它的最大端面吸力是受铁心饱和磁通密度所限。
铁心(及台座)端面的形状对吸力特性有较大的影响。锥顶铁心的吸力特性要比平顶的陡度小,如图1-19所示。因为锥顶气隙的磁导及其导数都比平顶气隙的大,在a较大时,可以认为线圈磁势绝大部分降落在主图1-20旋转式电磁铁 工作气隙上,即[厂nδ≈刀‰这时锥顶铁心的吸力就比平的静吸力特性顶的大;但当ε较小时,在铁磁阻和非工作气隙上的磁压降不能忽略,由于锥顶气隙的磁导比平顶气隙大,则在锥顶气隙上的磁压降就比平顶气隙小,所以锥顶铁心的吸力要比平顶铁心的小。显然,锥顶角α越小,即锥顶越尖时,吸力特性也就越平,ε较大时的吸力也越大,所以适用于需要较大行程的情况。
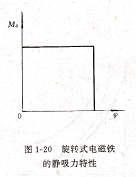
旋转式电磁铁的吸力特性,从式(1-18)可知,旋转式电磁铁在忽略铁磁阻以及线圈磁势J・″为常数时,ymδ和Md为常数,因此,电磁铁的吸力特性为一水平直线,如图1-20所示。图1-7所示的旋转式电磁铁只是一种特殊情况。在一般情况下气隙a不是常数而是根据吸力特性的要求,通过改变极面形状使其按一定规律变化。这时旋转式电磁铁的电磁转矩计算公式的推导可参阅王宝龄主编的《电磁电器设计基础》一书,这里不再论述。
W58-XB1A4A-4式中,Φδ的单位为Mx。
值得指出的是,麦克斯韦吸力公式和由能量守恒定律计算出来的吸力公式是可以互相转换的。但是麦克斯韦吸力公式适合于磁极间磁场均匀分布的情况。由于铁磁材料的导磁系数远比空气大得多,只要未达到饱和,磁力线可以认为是垂直于磁极表面的;而当气隙不大时,其分布又往往是比较均匀的。因此,用麦克斯韦公式可更方便地计算吸力,并且具有一定的精确度。
典型直流电磁铁的吸力特性,拍合式电磁铁的吸力特性,假如拍合式电磁铁吸片转动时,由于吸片转角α和气隙a一般都很小,为了大致看看吸力特性的变化规律,可以近似认为气隙磁导^δ=号气而代入式(1-10)得
另外,还可以忽略铁磁阻和非工作气隙的磁阻,则σ斋δ就近似等于线圈磁势rW而且不随气隙a的变化而变化。因此式(1-26)就可表为
Fd=c(rw)2 (N) (1~27)
式,(1-27)中设C=σ7)2踟S为常数,即不随气隙a而变化,那么有这是二次双曲线函数的关系,如图1-18中虚线1所示。

实际上,导磁体内总会有磁阻,所以tr缶δ不等于刀巳而是随a的减小而减小,因为ε减小时,磁通增大,导磁体内磁压降就会增大◇因此,实际的吸力特性偏离双曲线,a越小,导磁体的磁压降就越大,曲线偏离也越大,如图1-18中曲线2所示。 拍合式电磁铁的吸力特性,若忽略铁磁阻而假定饥nδccr″,则在某一气隙下,Fd∝σ″)2,即当磁势增大时,吸力特性上移,如图中曲线3所示。由于二次双曲线函数很陡,也就是说,拍合式电磁铁的吸力将随着气隙增大而减小很多,所以这种电磁铁不宜用于行程要求较大的情况。
E型拍合式电磁铁(图1-2(b))的吸力特性要比U型的更陡,即在闭合位置时,E型
的吸力比U型大得多,但在打开位置时,大得就不显著了。对于衔铁位于侧面的拍合式电磁铁(图1-3),其漏磁通通过吸片,因此还应该考虑漏磁通产生的力矩M洳,即Md=Mdδ+1f,式中Mdδ为主工作气隙磁通所产生的力矩。
吸入式电磁铁的吸力特性由前面分析可知,吸入式电磁铁的吸力计算公式为式(1-17)所表示。对于吸入式电磁铁的吸力特性有以下几个特点:
若铁心为平顶,则当ε不是很大时可以
认为^δ=u。苄(S为极面面积),而话等=Qa2,因此,Fdδ=r(a)的特性同拍合式相近,即随a的增大,Fdδ减小很多。但是,当a变化时,漏磁通Φσ1却改变不多(因为a的变化量相对Ja来说是不大的),所以Fdσ不会因a的增大而减小很多。这就使得吸入式电磁铁的吸力要比拍合式的大,并且,在打开位置时,螺管力 图1-19 吸人式电磁铁的静吸力特性所占的比例更大。因此,它适用于需要铁心行程较大的情况。
螺管力Fdc与线圈磁势σ″)2成正比,因此,增大IⅥ/就可以增大Fdσ・而不会受磁路饱和所限,这就使吸入式电磁铁适用于短时产生较大的吸力,因为线圈短时通以很大电流并不会发热过甚。而拍合式电磁铁没有这一特点,因为它的最大端面吸力是受铁心饱和磁通密度所限。
铁心(及台座)端面的形状对吸力特性有较大的影响。锥顶铁心的吸力特性要比平顶的陡度小,如图1-19所示。因为锥顶气隙的磁导及其导数都比平顶气隙的大,在a较大时,可以认为线圈磁势绝大部分降落在主图1-20旋转式电磁铁 工作气隙上,即[厂nδ≈刀‰这时锥顶铁心的吸力就比平的静吸力特性顶的大;但当ε较小时,在铁磁阻和非工作气隙上的磁压降不能忽略,由于锥顶气隙的磁导比平顶气隙大,则在锥顶气隙上的磁压降就比平顶气隙小,所以锥顶铁心的吸力要比平顶铁心的小。显然,锥顶角α越小,即锥顶越尖时,吸力特性也就越平,ε较大时的吸力也越大,所以适用于需要较大行程的情况。
旋转式电磁铁的吸力特性,从式(1-18)可知,旋转式电磁铁在忽略铁磁阻以及线圈磁势J・″为常数时,ymδ和Md为常数,因此,电磁铁的吸力特性为一水平直线,如图1-20所示。图1-7所示的旋转式电磁铁只是一种特殊情况。在一般情况下气隙a不是常数而是根据吸力特性的要求,通过改变极面形状使其按一定规律变化。这时旋转式电磁铁的电磁转矩计算公式的推导可参阅王宝龄主编的《电磁电器设计基础》一书,这里不再论述。





 公网安备44030402000607
公网安备44030402000607





