TP3057ADW 吸入式电磁铁
发布时间:2019/10/28 12:09:05 访问次数:857
TP3057ADW端面上的漏磁通Φd1与线圈导线电流作用而产生的电动力。Fdd也称为螺管力。端面吸力的计算可用公式1-10计算,即而螺管力Fdσ可以近似用下式计算,即
Fdσ=iwΦσ1 (N)(1-14)
式中 IW一线圈磁势(安匝);
Jk―线圈长度(m);
Φ1―可动铁心部分总编磁通(Wb)。
图1-16为吸入式电磁铁通过轴线的一个剖面,在其上半部画出了可动铁心段分布的漏磁通。该漏磁通对圆环导螺管力的计算线产生电动力力图使线圈右移(左手定则),而其反作用力却使可动铁心左移。
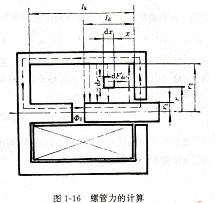
设伸入线圈内的可动铁心的长度为Ja,如果忽略铁磁阻及非工作气隙的磁阻,则在Ja段内总的漏磁通Φσ1为式中,^为可动铁心到壳体之间单位长度的漏磁导,可通过查表得到。因此,由通过可动铁心侧面的漏磁通Φσ1所产生的螺管力Fdσ为
Fdσ=1/2(r)2人(l1/lk)2 (N)
将式(1-13)及(1-16)代入式(1-12),最后得吸入式电磁铁的吸力计算公式:Fd=EU象δ告等一(r″)2入(舟)2] (N)
旋转式电磁铁的吸力计算公式,旋转式电磁铁的衔铁转动时,通常漏磁通的变化并不大,因此,可以用公式(1-11)来计算电磁力矩。它与拍合式电磁铁的不同点在于其衔铁运动的方向垂直于磁力线的方向。电磁力矩的方向总是力图使衔铁运动到使整个磁路内磁阻为最小的位置,因此,在图1-7所示的例子中,电磁力矩的方向为逆时针的方向。在这个例子中,当衔铁转动时,气隙aO并不变化,但气隙面积s将发生变化。如不考虑散磁,则气隙磁导^δ可由下式计算,即式中 α―极面对转轴所夹的角度(rad);
r0―极面圆弧的半径(m);
3一衔铁厚度(m)。
因为,衔铁旋转时上、下两个气隙的极面都发生变化,因此,电磁力矩为Md=2×扣跆=y廴呷 (N・m) (1-19)
式中,己/mδ为每一个气隙上的磁压降(安匝)。应注意的是在这里应用公式(1-11)时没有取负号,这是因为这里Md的正方向是逆时针方向,即逆时针方向转动α角时,可使整个磁路内的磁阻减小。
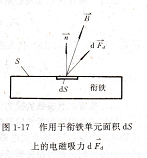
麦克斯韦吸力公式,电磁吸力也可利用麦克斯韦公式计算,如图1-17所示,作用于单元面积ds上的电磁力dFd及作用于整个衔铁上的合成力Fd为
dFd=E(y・i)B一rB2″]ds (1-20)
u=p6(Bop):―≡y2kηds (1~21)
式中B一元面积dS外方表面上的磁感应矢量;
″―元面积dS上单位外向法线单位矢量。
式(1―21)为矢量积分,积分面积应该与整个衔铁外表面吻合。用该公式所确定的吸力是各个单元表面吸力的矢量和,此公式适用于任何磁性物体。对于铁磁体,由于0,衔铁外表面的磁感应强度B都近似垂直积分表面.
TP3057ADW端面上的漏磁通Φd1与线圈导线电流作用而产生的电动力。Fdd也称为螺管力。端面吸力的计算可用公式1-10计算,即而螺管力Fdσ可以近似用下式计算,即
Fdσ=iwΦσ1 (N)(1-14)
式中 IW一线圈磁势(安匝);
Jk―线圈长度(m);
Φ1―可动铁心部分总编磁通(Wb)。
图1-16为吸入式电磁铁通过轴线的一个剖面,在其上半部画出了可动铁心段分布的漏磁通。该漏磁通对圆环导螺管力的计算线产生电动力力图使线圈右移(左手定则),而其反作用力却使可动铁心左移。

设伸入线圈内的可动铁心的长度为Ja,如果忽略铁磁阻及非工作气隙的磁阻,则在Ja段内总的漏磁通Φσ1为式中,^为可动铁心到壳体之间单位长度的漏磁导,可通过查表得到。因此,由通过可动铁心侧面的漏磁通Φσ1所产生的螺管力Fdσ为
Fdσ=1/2(r)2人(l1/lk)2 (N)
将式(1-13)及(1-16)代入式(1-12),最后得吸入式电磁铁的吸力计算公式:Fd=EU象δ告等一(r″)2入(舟)2] (N)
旋转式电磁铁的吸力计算公式,旋转式电磁铁的衔铁转动时,通常漏磁通的变化并不大,因此,可以用公式(1-11)来计算电磁力矩。它与拍合式电磁铁的不同点在于其衔铁运动的方向垂直于磁力线的方向。电磁力矩的方向总是力图使衔铁运动到使整个磁路内磁阻为最小的位置,因此,在图1-7所示的例子中,电磁力矩的方向为逆时针的方向。在这个例子中,当衔铁转动时,气隙aO并不变化,但气隙面积s将发生变化。如不考虑散磁,则气隙磁导^δ可由下式计算,即式中 α―极面对转轴所夹的角度(rad);
r0―极面圆弧的半径(m);
3一衔铁厚度(m)。
因为,衔铁旋转时上、下两个气隙的极面都发生变化,因此,电磁力矩为Md=2×扣跆=y廴呷 (N・m) (1-19)
式中,己/mδ为每一个气隙上的磁压降(安匝)。应注意的是在这里应用公式(1-11)时没有取负号,这是因为这里Md的正方向是逆时针方向,即逆时针方向转动α角时,可使整个磁路内的磁阻减小。
麦克斯韦吸力公式,电磁吸力也可利用麦克斯韦公式计算,如图1-17所示,作用于单元面积ds上的电磁力dFd及作用于整个衔铁上的合成力Fd为
dFd=E(y・i)B一rB2″]ds (1-20)
u=p6(Bop):―≡y2kηds (1~21)
式中B一元面积dS外方表面上的磁感应矢量;
″―元面积dS上单位外向法线单位矢量。

式(1―21)为矢量积分,积分面积应该与整个衔铁外表面吻合。用该公式所确定的吸力是各个单元表面吸力的矢量和,此公式适用于任何磁性物体。对于铁磁体,由于0,衔铁外表面的磁感应强度B都近似垂直积分表面.
上一篇:AS3931DB石英晶体振荡器



 公网安备44030402000607
公网安备44030402000607





