SP6656ER3-L 各门电路输出的波形
发布时间:2020/2/8 17:39:12 访问次数:1517
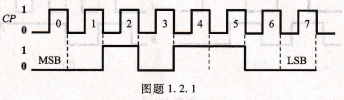
SP6656ER3-L数制一数字波形如图题1.2.1所示,时钟频率为4 kHz,试确定:(1)它所表示的二进制数;(2)串行方式传送8位数据所需要的时间;(3)以8位并行方式传送数据时需要的时间。
1.2.2 将下列十进制数转换为二进制数、八进制数和十六进制数(要求转换误差不大于2-4):
(1)43 (2)127 (3)254.25 (4)2,718
1.2.3 将下列二进制数转换为十六进制数:
(1) (101001): (2) (11.01101):
1.2.4 将下列十进制数转换为十六进制数(要求转换误差不大于16-4):
(1) (500)D (2) (59)D (3) (0.34)D (4) (1002,45)D
1.2.5 将下列十六制数转换为二进制数:
(1) (23F.45)Ⅱ (2) (A040,51)Ⅱ
1.2.6 将下列十六进制数转换为十进制数:
(1) (103,2)Ⅱ (2) (A45D.0BC)H
1.3 二进制数的算术运算
1.3.1 写出下列二进制数的原码、反码和补码:
(1) ( +1110): (2) ( +10110): (3) ( -1110): (4) ( -10110):
1.3.2 写出下列有符号二进制补码所表示的十进制数:
(1) 0010111 (2) 11101000
1.3.3 试用8位二进制补码计算下列各式,并用十进制数表示结果:
(1) 12+9 (2) 11-3 (3) -29-25 (4) -120+30
1.4 二进制代码
1.4.1 将下列十进制数转换为8421BCD码:
(1) 43 (2) 127 (3) 254.25 (4) 2.718
1.4.2 将下列数码作为自然二进制数或8421BCD码时,分别求出相应的十进制数:
(1)1(X)10111 (2)1⑾01(X)1(X)11 (3)(XX)101(X)1(X)1 (4)1(XXX)1(X).1(X)1(XX)1
1.4.3 试用十六进制数写出下列字符的ASCII码的表示:
(1) + (2)@ (3)you (4)43
1.6 逻辑函数及其表示方法
1.6.1 在图题1.6.1中,已知输入信号A、B的波形,画出各门电路输出z的波形。
则A+A=0+0=0=A; 除此之外,别无其他可能,可见A+c=A。
在以上所有定律中,反演律具有特殊重要的意义。反演律又称为摩根定理,它经常用于求一个原函数的非函数或者对逻辑函数进行变换。为了证明A+B=AB,AB=A+B,按A、B所有可能的取值情况列出真值表,如表2.1.2所示。将表中第3列和第4列进行比较、第5列和第6列进行比较,可见等式两边的真值表相同,故等式成立。
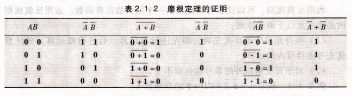
表2.1.2 摩根定理的证明
AB+c
=AB(1+C)+AC(1+B)
=aB+AC
这个恒等式说明,若两个乘积项中分别包含因子A和A,而这两个乘积项的其余因子组成第三个乘积项时,则第二个乘积项是多余的,可以消去。
本节所列出的基本公式反映了逻辑关系,而不是数量之间的关系,在运算中不能简单套用初等代数的运算规则。例如初等代数中的移项规则就不能用,这是因为逻辑代数中没有减法和除法的缘故。这一点在使用时必须注意。
逻辑代数的基本规则,代入规则,在任何一个逻辑等式中,如果将等式两边出现的某变量Ab,都用一个函数代替,则等式依然成立,这个规则称为代入规则。
例如,在B(A+C)=B4+BC中,将所有出现A的地方都用函数E+F代替,则等式仍成立,即得
aB[(E+F)+C]=B(E+F)+BC=BE+BF+BC
代人规则可以扩展所有基本定律或定理的应用范围。例如前面用真值表证明了用二变量表示的摩根定理AB=A+B,若用L=CD代替等式中的A,则AB=A+B
表2.1.1中的常用恒等式可以用其他基本定律加以证明,下面证明其中的第一条逻辑代数.
深圳市唯有度科技有限公司http://wydkj.51dzw.com/
SP6656ER3-L数制一数字波形如图题1.2.1所示,时钟频率为4 kHz,试确定:(1)它所表示的二进制数;(2)串行方式传送8位数据所需要的时间;(3)以8位并行方式传送数据时需要的时间。

1.2.2 将下列十进制数转换为二进制数、八进制数和十六进制数(要求转换误差不大于2-4):
(1)43 (2)127 (3)254.25 (4)2,718
1.2.3 将下列二进制数转换为十六进制数:
(1) (101001): (2) (11.01101):
1.2.4 将下列十进制数转换为十六进制数(要求转换误差不大于16-4):
(1) (500)D (2) (59)D (3) (0.34)D (4) (1002,45)D
1.2.5 将下列十六制数转换为二进制数:
(1) (23F.45)Ⅱ (2) (A040,51)Ⅱ
1.2.6 将下列十六进制数转换为十进制数:
(1) (103,2)Ⅱ (2) (A45D.0BC)H
1.3 二进制数的算术运算
1.3.1 写出下列二进制数的原码、反码和补码:
(1) ( +1110): (2) ( +10110): (3) ( -1110): (4) ( -10110):
1.3.2 写出下列有符号二进制补码所表示的十进制数:
(1) 0010111 (2) 11101000
1.3.3 试用8位二进制补码计算下列各式,并用十进制数表示结果:
(1) 12+9 (2) 11-3 (3) -29-25 (4) -120+30
1.4 二进制代码
1.4.1 将下列十进制数转换为8421BCD码:
(1) 43 (2) 127 (3) 254.25 (4) 2.718
1.4.2 将下列数码作为自然二进制数或8421BCD码时,分别求出相应的十进制数:
(1)1(X)10111 (2)1⑾01(X)1(X)11 (3)(XX)101(X)1(X)1 (4)1(XXX)1(X).1(X)1(XX)1
1.4.3 试用十六进制数写出下列字符的ASCII码的表示:
(1) + (2)@ (3)you (4)43
1.6 逻辑函数及其表示方法
1.6.1 在图题1.6.1中,已知输入信号A、B的波形,画出各门电路输出z的波形。
则A+A=0+0=0=A; 除此之外,别无其他可能,可见A+c=A。
在以上所有定律中,反演律具有特殊重要的意义。反演律又称为摩根定理,它经常用于求一个原函数的非函数或者对逻辑函数进行变换。为了证明A+B=AB,AB=A+B,按A、B所有可能的取值情况列出真值表,如表2.1.2所示。将表中第3列和第4列进行比较、第5列和第6列进行比较,可见等式两边的真值表相同,故等式成立。

表2.1.2 摩根定理的证明
AB+c
=AB(1+C)+AC(1+B)
=aB+AC
这个恒等式说明,若两个乘积项中分别包含因子A和A,而这两个乘积项的其余因子组成第三个乘积项时,则第二个乘积项是多余的,可以消去。
本节所列出的基本公式反映了逻辑关系,而不是数量之间的关系,在运算中不能简单套用初等代数的运算规则。例如初等代数中的移项规则就不能用,这是因为逻辑代数中没有减法和除法的缘故。这一点在使用时必须注意。
逻辑代数的基本规则,代入规则,在任何一个逻辑等式中,如果将等式两边出现的某变量Ab,都用一个函数代替,则等式依然成立,这个规则称为代入规则。
例如,在B(A+C)=B4+BC中,将所有出现A的地方都用函数E+F代替,则等式仍成立,即得
aB[(E+F)+C]=B(E+F)+BC=BE+BF+BC
代人规则可以扩展所有基本定律或定理的应用范围。例如前面用真值表证明了用二变量表示的摩根定理AB=A+B,若用L=CD代替等式中的A,则AB=A+B
表2.1.1中的常用恒等式可以用其他基本定律加以证明,下面证明其中的第一条逻辑代数.
深圳市唯有度科技有限公司http://wydkj.51dzw.com/



 公网安备44030402000607
公网安备44030402000607





