XC61AN1102PR摩根定理
发布时间:2019/10/25 12:35:54 访问次数:1160
XC61AN1102PRs1状态:主干道黄灯亮,支干道红灯亮,进人此状态,黄灯亮足规定的时间间隔rY时,控制器发出状态转换信号sT,输出从状态sI转换到S2。
S2状态:支干道绿灯亮,主干道红灯亮,若此时支干道继续有车,则继续保持此状态,但支干道绿灯亮的时间不得超过rs时间间隔,否则控制单元发出状态转换信号sT,使输出转换到S3状态。
S3状态:支干道黄灯亮,主干道红灯亮,此时状态与sl状态持续的时间间隔相同,均为rY,时间到时,控制器发出ST信号,输出从状态s3回到so状态。
对上述sO、s1、s2和S3四种状态按照格雷码进行编码分别为00、01、11和10,由此得到交通灯控制单元的ASM图,如图10,2.7所示。异步复位信号Rese莎使控制单元直接进人主干道绿灯亮、支干道红灯亮的初始状态,用s。状态框表示。当s。状态持续时间TL大于等于60s,并且支干道有车等待通过,传感器s=1时,此时满足判断框中的rL・s=1条件,控制单元发出状态转换信号sT,由条件输出框表示,同时系统从状态sO转到主干道黄灯亮、支干道红灯亮的sl状态。依此类推得出图10.2.7所示的ASM图。
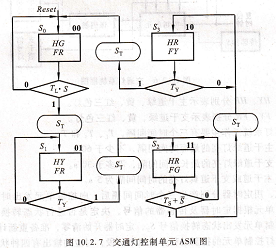
根据交通灯控制单元的ASM图,得出其状态图,如图10.2.8所示。ASM图中的状态框与状态图中的状态相对应,判断框中的条件是状态转换的输人条件,条仵输出框与控制单元状态转换的输出相对应。状态图描述状态之间的转换,例如在sO状态,如果rL・s=1,则系统状态转移到sl,同时输出状态转则A+A=0+0=0=A; 除此之外,别无其他可能,可见A+姓=A。
在以上所有定律中,反演律具有特殊重要的意义。反演律又称为摩根定理,它经常用于求一个原函数的非函数或者对逻辑函数进行变换。为了证明A+B=AB,AB=A+B,按A、B所有可能的取值情况列出真值表,如表2.1.2所示。将表中第3列和第4列进行比较、第5列和第6列进行比较,可见等式两边的真值表相同,故等式成立。
表2.1.2 摩根定理的证明
AB+⒕
=AB(1+C)+AC(1+B)
=B+AC ・
这个恒等式说明,若两个乘积项中分别包含因子A和A,而这两个乘积项的其余因子组成第三个乘积项时,则第二个乘积项是多余的,可以消去。本节所列出的基本公式反映了逻辑关系,而不是数量之间的关系,在运算中不能简单套用初等代数的运算规则。例如初等代数中的移项规则就不能用,这是因为逻辑代数中没有减法和除法的缘故。这一点在使用时必须注意。
逻辑代数的基本规则
1.代入规则,在任何一个逻辑等式中,如果将等式两边出现的某变量A^,都用一个函数代替,则等式依然成立,这个规则称为代入规则。
例如,在B(A+C)=B4+BC中,将所有出现A的地方都用函数E+F代替”则等式仍成立,即得
B[(E+F)+C]=B(E+F)+BC=BE+BF+BC
代人规则可以扩展所有基本定律或定理的应用范围。例如前面用真值表证明了用二变量表示的摩根定理AB=A+B,若用L=CD代替等式中的A.
XC61AN1102PRs1状态:主干道黄灯亮,支干道红灯亮,进人此状态,黄灯亮足规定的时间间隔rY时,控制器发出状态转换信号sT,输出从状态sI转换到S2。
S2状态:支干道绿灯亮,主干道红灯亮,若此时支干道继续有车,则继续保持此状态,但支干道绿灯亮的时间不得超过rs时间间隔,否则控制单元发出状态转换信号sT,使输出转换到S3状态。
S3状态:支干道黄灯亮,主干道红灯亮,此时状态与sl状态持续的时间间隔相同,均为rY,时间到时,控制器发出ST信号,输出从状态s3回到so状态。
对上述sO、s1、s2和S3四种状态按照格雷码进行编码分别为00、01、11和10,由此得到交通灯控制单元的ASM图,如图10,2.7所示。异步复位信号Rese莎使控制单元直接进人主干道绿灯亮、支干道红灯亮的初始状态,用s。状态框表示。当s。状态持续时间TL大于等于60s,并且支干道有车等待通过,传感器s=1时,此时满足判断框中的rL・s=1条件,控制单元发出状态转换信号sT,由条件输出框表示,同时系统从状态sO转到主干道黄灯亮、支干道红灯亮的sl状态。依此类推得出图10.2.7所示的ASM图。

根据交通灯控制单元的ASM图,得出其状态图,如图10.2.8所示。ASM图中的状态框与状态图中的状态相对应,判断框中的条件是状态转换的输人条件,条仵输出框与控制单元状态转换的输出相对应。状态图描述状态之间的转换,例如在sO状态,如果rL・s=1,则系统状态转移到sl,同时输出状态转则A+A=0+0=0=A; 除此之外,别无其他可能,可见A+姓=A。
在以上所有定律中,反演律具有特殊重要的意义。反演律又称为摩根定理,它经常用于求一个原函数的非函数或者对逻辑函数进行变换。为了证明A+B=AB,AB=A+B,按A、B所有可能的取值情况列出真值表,如表2.1.2所示。将表中第3列和第4列进行比较、第5列和第6列进行比较,可见等式两边的真值表相同,故等式成立。
表2.1.2 摩根定理的证明
AB+⒕
=AB(1+C)+AC(1+B)
=B+AC ・
这个恒等式说明,若两个乘积项中分别包含因子A和A,而这两个乘积项的其余因子组成第三个乘积项时,则第二个乘积项是多余的,可以消去。本节所列出的基本公式反映了逻辑关系,而不是数量之间的关系,在运算中不能简单套用初等代数的运算规则。例如初等代数中的移项规则就不能用,这是因为逻辑代数中没有减法和除法的缘故。这一点在使用时必须注意。
逻辑代数的基本规则
1.代入规则,在任何一个逻辑等式中,如果将等式两边出现的某变量A^,都用一个函数代替,则等式依然成立,这个规则称为代入规则。
例如,在B(A+C)=B4+BC中,将所有出现A的地方都用函数E+F代替”则等式仍成立,即得
B[(E+F)+C]=B(E+F)+BC=BE+BF+BC
代人规则可以扩展所有基本定律或定理的应用范围。例如前面用真值表证明了用二变量表示的摩根定理AB=A+B,若用L=CD代替等式中的A.




 公网安备44030402000607
公网安备44030402000607





