TC74ACT02FS各种逻辑框之间的时间关系
发布时间:2019/10/25 12:19:38 访问次数:835
TC74ACT02FS沿的触发下,控制单元离开状态sl,因此一个状态框占用一个时钟脉冲周期。
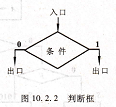
判断框表示ASM图的状态分支,如图10.2.2所示,它有一个人口和多个出口,框内填判断条件,如果条件是真,选择一个出口,若条件是假,选择另一个出口。
判断框的入口来自某一个状态框,在该状态占用的一个时钟周期内,根据判断框中的条件,以决定下一个时钟脉冲触发沿来到时,该状态从判断框的哪个出口出去,因此,判断框不占用时间。
条件输出框如图10.2.3(a)所示,条件框的入口必定与判断框的输出相连。列在条件框内的寄存器(R)操作或输出是在给定的状态下,满足判断条件才发生的。在图10,2,3(b)的例子中,当系统处于状态S1时,若条件X=1,则R被清0,否则R保持不变;不论X为何值,系统的下一个状态都是s2。
各种逻辑框之间的时间关系从表面上来看AsM图与程序流程图很相似,但实际上有很大的差异。程序流程图只表示事件发生的先后顺序,没有时间概念,而AsM图则不同,它表示事件的精确时间顺序。在ASM图中每一个状(a)(b)态框表示一个时间周期内的系统状态,状态框和与之相连的判断框,条件输出框所 条件输出框与实例,规定的操作,都是在一个共同的时钟周期实现的,同时系统的控制器从现在状态(现态)转移到下一个状态(次态)。因此,可以很容易将图10.2.4(a)所示的ASM图,转换成状态图,如图10.2.4(b)所示,其中E和F为状态转换条件。与ASM图不同,状态图无法表示寄存器操作。
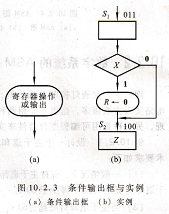
图10.2.4(c)所示为ASM图的各种操作及状态转换的时间图。假设系统中所有触发器都是上升沿触废的,在第一个时钟脉冲上升沿来到时,系统转换到s。状态,随后根据条件由判断框输出1(真)或0(假),以便在下一个时钟脉冲上升沿到达时,系统的状态由s0转换到Sl、S2和S3中的一个。
代数的基本定律和恒等式,1章介绍过的逻辑与、或、非三种基本运算法则可以推导出下面常代数基本定律和恒等式,如表2.1.1所示。
对表2.1.1所示定律和定理的证明方法是:列出等式左边函数与右边函数的真值表,如果等式两边的真值表相同,说明等式成立。
例如,要证明处+A=A时,令A=1,则A+⒕=1+1=1=处;再令姓=0,
系De M。gen的译称。
逻辑代数与硬件描述语言基,逻辑代数是1854年问世的,早年用于开关和继电器网络的分析、化简,随着半导体器件制造工艺的发展,各种具有良好开关性能的微电子器件不断涌现,因而逻辑代数已成为分析和设计现代数字逻辑电路不可缺少的数学工具。逻辑代数有一系列的定律、定理和规则,用它们对数学表达式进行处理,可以完成对逻辑电路的化简、变换、分析和设计。
TC74ACT02FS沿的触发下,控制单元离开状态sl,因此一个状态框占用一个时钟脉冲周期。
判断框表示ASM图的状态分支,如图10.2.2所示,它有一个人口和多个出口,框内填判断条件,如果条件是真,选择一个出口,若条件是假,选择另一个出口。
判断框的入口来自某一个状态框,在该状态占用的一个时钟周期内,根据判断框中的条件,以决定下一个时钟脉冲触发沿来到时,该状态从判断框的哪个出口出去,因此,判断框不占用时间。

条件输出框如图10.2.3(a)所示,条件框的入口必定与判断框的输出相连。列在条件框内的寄存器(R)操作或输出是在给定的状态下,满足判断条件才发生的。在图10,2,3(b)的例子中,当系统处于状态S1时,若条件X=1,则R被清0,否则R保持不变;不论X为何值,系统的下一个状态都是s2。
各种逻辑框之间的时间关系从表面上来看AsM图与程序流程图很相似,但实际上有很大的差异。程序流程图只表示事件发生的先后顺序,没有时间概念,而AsM图则不同,它表示事件的精确时间顺序。在ASM图中每一个状(a)(b)态框表示一个时间周期内的系统状态,状态框和与之相连的判断框,条件输出框所 条件输出框与实例,规定的操作,都是在一个共同的时钟周期实现的,同时系统的控制器从现在状态(现态)转移到下一个状态(次态)。因此,可以很容易将图10.2.4(a)所示的ASM图,转换成状态图,如图10.2.4(b)所示,其中E和F为状态转换条件。与ASM图不同,状态图无法表示寄存器操作。

图10.2.4(c)所示为ASM图的各种操作及状态转换的时间图。假设系统中所有触发器都是上升沿触废的,在第一个时钟脉冲上升沿来到时,系统转换到s。状态,随后根据条件由判断框输出1(真)或0(假),以便在下一个时钟脉冲上升沿到达时,系统的状态由s0转换到Sl、S2和S3中的一个。
代数的基本定律和恒等式,1章介绍过的逻辑与、或、非三种基本运算法则可以推导出下面常代数基本定律和恒等式,如表2.1.1所示。
对表2.1.1所示定律和定理的证明方法是:列出等式左边函数与右边函数的真值表,如果等式两边的真值表相同,说明等式成立。
例如,要证明处+A=A时,令A=1,则A+⒕=1+1=1=处;再令姓=0,
系De M。gen的译称。
逻辑代数与硬件描述语言基,逻辑代数是1854年问世的,早年用于开关和继电器网络的分析、化简,随着半导体器件制造工艺的发展,各种具有良好开关性能的微电子器件不断涌现,因而逻辑代数已成为分析和设计现代数字逻辑电路不可缺少的数学工具。逻辑代数有一系列的定律、定理和规则,用它们对数学表达式进行处理,可以完成对逻辑电路的化简、变换、分析和设计。


 公网安备44030402000607
公网安备44030402000607





