窗函数
发布时间:2012/10/21 16:13:22 访问次数:1334
推荐使用汉宁( Hanning)窗。如因需要采K4M28323LH-HN75用其他谱图,应加以说明。
对一个时间函数进行离散的傅里叶变换,只能取有限个采样点,即一定要将时域函数截断。这样就产生了泄漏,即能量“泄漏”到其他一些频率成分上去了。图3-35中对两个周期稍有不同的正弦信号进行分析:对图3-35 (a)所示情况,在采样周期丁中,正好包含3个信号的完整周期,经变换后谱线很简单,只得到一等于正弦信号频率的谱线;对图3-35 (b)所示情况,由于在采样周期丁中,不是正好包含信号的4个完整的周期,谱线不是显示信号的单一频率,而是扩展成几条谱线,说明产生了泄漏。
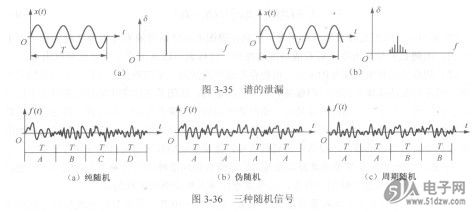
由此可见,对于x(t)是周期函数的,假如在截断函数的长度丁内包含x(t)的胛个完整的周期(即是整数),则可避免泄漏。这也是解决泄漏的一个方法。所以在随机激励时采用如图3-36所示的伪随机信号、周期随机信号都能减小泄漏误差。从3-36 (a)可见,纯随机信号是白噪声,其能量分布在很宽的频段内,功率谱是平的,每个测量周期内的样本函数都不相同,所以每次测试结果中的非线性畸变的影响及噪声均不同,经多次平均后可消除噪声干扰及非线性畸变,但由于信号不具有周期性,易产生泄漏,致使处理精度降低;图3-36 (b)中的伪随机信号具有周期性,在测量时间内的信号是随机的,各次测量时间内又是完全相同的,所以具有周期性,周期与分析仪的采样时间相配合,因此能避免产生泄漏,但由于每段采样的又都是相同的信号,所以不能用多次平均来消除噪声干扰及非线性畸变;图3-36 (c)中的周期随机信号是每两段均一样,两段与两段是不相关的随机信号,周期随机信号具有纯随机信号和伪随机信号共同的特点,信号既具有周期性,每两段样本又不一样,又具有随机性,所以既可消除泄漏误差,又可通过多次平均来消除噪声干扰等。
推荐使用汉宁( Hanning)窗。如因需要采K4M28323LH-HN75用其他谱图,应加以说明。
对一个时间函数进行离散的傅里叶变换,只能取有限个采样点,即一定要将时域函数截断。这样就产生了泄漏,即能量“泄漏”到其他一些频率成分上去了。图3-35中对两个周期稍有不同的正弦信号进行分析:对图3-35 (a)所示情况,在采样周期丁中,正好包含3个信号的完整周期,经变换后谱线很简单,只得到一等于正弦信号频率的谱线;对图3-35 (b)所示情况,由于在采样周期丁中,不是正好包含信号的4个完整的周期,谱线不是显示信号的单一频率,而是扩展成几条谱线,说明产生了泄漏。

由此可见,对于x(t)是周期函数的,假如在截断函数的长度丁内包含x(t)的胛个完整的周期(即是整数),则可避免泄漏。这也是解决泄漏的一个方法。所以在随机激励时采用如图3-36所示的伪随机信号、周期随机信号都能减小泄漏误差。从3-36 (a)可见,纯随机信号是白噪声,其能量分布在很宽的频段内,功率谱是平的,每个测量周期内的样本函数都不相同,所以每次测试结果中的非线性畸变的影响及噪声均不同,经多次平均后可消除噪声干扰及非线性畸变,但由于信号不具有周期性,易产生泄漏,致使处理精度降低;图3-36 (b)中的伪随机信号具有周期性,在测量时间内的信号是随机的,各次测量时间内又是完全相同的,所以具有周期性,周期与分析仪的采样时间相配合,因此能避免产生泄漏,但由于每段采样的又都是相同的信号,所以不能用多次平均来消除噪声干扰及非线性畸变;图3-36 (c)中的周期随机信号是每两段均一样,两段与两段是不相关的随机信号,周期随机信号具有纯随机信号和伪随机信号共同的特点,信号既具有周期性,每两段样本又不一样,又具有随机性,所以既可消除泄漏误差,又可通过多次平均来消除噪声干扰等。




 公网安备44030402000607
公网安备44030402000607





