GAL16V8-25QVC互补对称电路的输出功率
发布时间:2019/11/9 17:46:18 访问次数:2187
GAL16V8-25QVC两射极输出器组成的基本互补对称电路,(a)基本互补对称电路 (b)由NPN管组成的射极输出器,(c)由PNP管组成的射极输出器
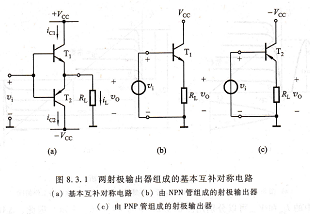
分析计算,图8,3.2a表示图8.3.1a电路在vi为正半周时T1的工作情况。图中假定,
只要ubE>0,T1就开始导电,则在一周期内T1导电时间约为半周期。图8,3.1a中T2的工作情况和T1相似,只是在信号的负半周导电。为了便于分析,将T2的特性曲线倒置在T1的右下方,并令二者在q点即ucE=ycc处重合,形成T1和T2的所谓合成曲线,如图8.3.2b所示。这时负载线通过ycc点形成一条斜线,其斜率为-1/rl。显然,允许的ic的最大变化范围为2icm,vcE的变化范围为2(ycc-7cEs)=2ycem=2rcm RL。如果忽略管子的饱和压降ycEs,则ycem=FemRL≈ycc。
根据以上分析,不难求出工作在乙类的互补对称电路的输出功率、管耗、直流电源供给的功率和效率。
输出功率用输出电压有效值vo和输出电流有效值fo的乘积来表示。设输出电压的幅值为vom,则
Po=voio=vom/2・vom/2rl=1/2・vom2/rl (⒏3.1)
图8.3.1中的T1、T2可以看成工作在射极输出器状态,Av≈1。当输人信号足够大,使yim=vom=ycc~ycEs≈ycc和rom=fcm时,可获得最大输出功率
pom=1/2・vom2/rl=1/2・vcem/rl=1/2・vcc2/rl (8.3.2)
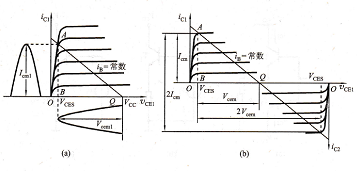
互补对称电路图解分析,(a)图8.3.1a电路ui为正半周时T1管工作情况, (b)互补对称电路工作情况,上式中的rcm和ycem可以分别用图8.3.2b中的AB和BO表示,因此,ΔABO的面积就代表了工作在乙类的互补对称电路输出功率的大小,ΔABO的面积越大,就表明输出功率Po也愈大。必须注意,对应于图8,3.2b的负载线Aq,
其功率三角形面积最大,非线性失真不明显,这是一种较理想的工作状态,但可惜的是,负载rl是固定的,不能随意改变,因而很难达到这种理想情况,除非采用变压器耦合,将实际负载RL变换成所期望的值Rl,以实现阻抗匹配.(见习题8.4.9)
管耗PT,考虑到T1和T2在一个信号周期内各导电约180°,且通过两管的电流和两
管两端的电压ocE在数值上都分别相等(只是在时间上错开了半个周期)。因此,为求出总管耗,只需先求出单管的损耗就行了。设输出电压为vo=yomsin ωt,则Tl的管耗为
PT1=1/2t0(vcc-uo)uo/rld(wt)
=1/2π(ycc-yomsin ωJ) (⒏3.3)
而两管的管耗为
pt=pt1=pt2
乙类的互补对称电非线性,这是一种理想的工显功率放大电路,除非采用变压器配。
直流电源供给的功率Pv,直流电源供给的功率Pv包括负载得到的信号功率T1、T2消耗的功率两部分。
当ui=0时,Pv=0;当vi≠0,由式(8.3.1)和式(8.3.4)得
Pv=Po+PT
=2vccyom/trl (⒏3.5)
πRL当输出电压幅值达到最大,即yom≈ycc时,则得电源供给的最大功率为
2π=Pvm
效率η,一般情况下效率为
η=Po/pv=t/4・vom/vcc
当vom≈ycc时,则
η=po/pv=t/4=78.5% (8.3.8)
这个结论是假定互补对称电路工作在乙类、负载电阻为理想值,忽略管子的饱和压降ycEs和输入信号足够大(yim≈vom≈ycc)情况下得来的,实际效率比这个数值要低些。
功率BJT的选择,最大管耗和最大输出功率的关系,工作在乙类的基本互补对称电路,在静态时,管子几乎不取电流,管耗接近于零,因此,当输人信号较小时,输出功率较小,管耗也小,这是容易理解的;但能否认为,当输人信号愈大,输出功率也愈大,管耗就愈大呢?答案是否定的G那么,最大管耗发生在什么情况下呢?由式(8.3.3)知,管耗PT1是输出电压幅值yom的函数,因此,可以用求极值的方法来求解。由式(⒏3.3)有
dPT1/dvom=1/rl(vcc/t-vom/2)
令dPT1/dvom=0,则vcc/t-vom/2=0
深圳市唯有度科技有限公司http://wydkj.51dzw.com/
GAL16V8-25QVC两射极输出器组成的基本互补对称电路,(a)基本互补对称电路 (b)由NPN管组成的射极输出器,(c)由PNP管组成的射极输出器

分析计算,图8,3.2a表示图8.3.1a电路在vi为正半周时T1的工作情况。图中假定,
只要ubE>0,T1就开始导电,则在一周期内T1导电时间约为半周期。图8,3.1a中T2的工作情况和T1相似,只是在信号的负半周导电。为了便于分析,将T2的特性曲线倒置在T1的右下方,并令二者在q点即ucE=ycc处重合,形成T1和T2的所谓合成曲线,如图8.3.2b所示。这时负载线通过ycc点形成一条斜线,其斜率为-1/rl。显然,允许的ic的最大变化范围为2icm,vcE的变化范围为2(ycc-7cEs)=2ycem=2rcm RL。如果忽略管子的饱和压降ycEs,则ycem=FemRL≈ycc。
根据以上分析,不难求出工作在乙类的互补对称电路的输出功率、管耗、直流电源供给的功率和效率。
输出功率用输出电压有效值vo和输出电流有效值fo的乘积来表示。设输出电压的幅值为vom,则
Po=voio=vom/2・vom/2rl=1/2・vom2/rl (⒏3.1)
图8.3.1中的T1、T2可以看成工作在射极输出器状态,Av≈1。当输人信号足够大,使yim=vom=ycc~ycEs≈ycc和rom=fcm时,可获得最大输出功率
pom=1/2・vom2/rl=1/2・vcem/rl=1/2・vcc2/rl (8.3.2)

互补对称电路图解分析,(a)图8.3.1a电路ui为正半周时T1管工作情况, (b)互补对称电路工作情况,上式中的rcm和ycem可以分别用图8.3.2b中的AB和BO表示,因此,ΔABO的面积就代表了工作在乙类的互补对称电路输出功率的大小,ΔABO的面积越大,就表明输出功率Po也愈大。必须注意,对应于图8,3.2b的负载线Aq,
其功率三角形面积最大,非线性失真不明显,这是一种较理想的工作状态,但可惜的是,负载rl是固定的,不能随意改变,因而很难达到这种理想情况,除非采用变压器耦合,将实际负载RL变换成所期望的值Rl,以实现阻抗匹配.(见习题8.4.9)
管耗PT,考虑到T1和T2在一个信号周期内各导电约180°,且通过两管的电流和两
管两端的电压ocE在数值上都分别相等(只是在时间上错开了半个周期)。因此,为求出总管耗,只需先求出单管的损耗就行了。设输出电压为vo=yomsin ωt,则Tl的管耗为
PT1=1/2t0(vcc-uo)uo/rld(wt)
=1/2π(ycc-yomsin ωJ) (⒏3.3)
而两管的管耗为
pt=pt1=pt2
乙类的互补对称电非线性,这是一种理想的工显功率放大电路,除非采用变压器配。
直流电源供给的功率Pv,直流电源供给的功率Pv包括负载得到的信号功率T1、T2消耗的功率两部分。
当ui=0时,Pv=0;当vi≠0,由式(8.3.1)和式(8.3.4)得
Pv=Po+PT
=2vccyom/trl (⒏3.5)
πRL当输出电压幅值达到最大,即yom≈ycc时,则得电源供给的最大功率为
2π=Pvm
效率η,一般情况下效率为
η=Po/pv=t/4・vom/vcc
当vom≈ycc时,则
η=po/pv=t/4=78.5% (8.3.8)
这个结论是假定互补对称电路工作在乙类、负载电阻为理想值,忽略管子的饱和压降ycEs和输入信号足够大(yim≈vom≈ycc)情况下得来的,实际效率比这个数值要低些。
功率BJT的选择,最大管耗和最大输出功率的关系,工作在乙类的基本互补对称电路,在静态时,管子几乎不取电流,管耗接近于零,因此,当输人信号较小时,输出功率较小,管耗也小,这是容易理解的;但能否认为,当输人信号愈大,输出功率也愈大,管耗就愈大呢?答案是否定的G那么,最大管耗发生在什么情况下呢?由式(8.3.3)知,管耗PT1是输出电压幅值yom的函数,因此,可以用求极值的方法来求解。由式(⒏3.3)有
dPT1/dvom=1/rl(vcc/t-vom/2)
令dPT1/dvom=0,则vcc/t-vom/2=0
深圳市唯有度科技有限公司http://wydkj.51dzw.com/



 公网安备44030402000607
公网安备44030402000607





