3NA3354-6继电器线圈电流的增长曲线
发布时间:2019/10/29 17:47:14 访问次数:1667
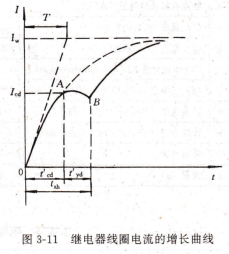
电磁继电器的吸合过程和吸合时间,电磁继电器的线圈电路具有一定电感量,在线圈两端加上直流电压[/后,电路中的电J不能跃升至稳态值rw(rw=σ/R,R为线圈电路的电阻值),而是随时间彦按一定的规律上升,如图3-11所示。因此,电磁铁的吸合过程可以分为两个阶段:一个是电流从零开始
上升到触动电流rcd,在这个阶段内衔铁没有运动,所需的时间r′cd称为吸合触动时间。当电流值达到rcd以后,吸力Fd将大于反力F”衔铁开始运动。衔铁运动以后,电流的变化规律变得复杂。从衔铁开始运动到最后达到闭合位置所需的时间hd称为吸合运动时间。因此,电磁继电器的固有吸合时间莎xh包括两部分,即
txh=t′cd+t′yd (3-1)
下面对这两个阶段分别进行一些讨论。
吸合触动时间t′cd
当线圈加上直流电压【厂以后,其电流(或磁通)增长的过渡过程可以由电压平衡方程求得,即
u=ir+d/dt (3-2)
式中 u一线圈电压(V);
i一线圈电流(A);
R――线圈回路总电阻(Ω);
d一线圈总的磁链(Wb);
t一通电时间(s)。
当衔铁处于打开位置时,并且电流又不很大,磁路一般并不饱和,则可以认为线圈电感L为常数,则式(3-2)可改写为
u=iR+Ldi/dt (3-3)
而式(3-3)的解为
i=iw(1-e-t/t) (3-4)
式中 iw一线圈的稳态电流,rw=y/R(A);
T一线圈的电时间常数,T=L/R(s)。
可见1电流按指数曲线上升,如图3-11。假如电流达到fed后衔铁仍保持不动,则电流将按照图中虚线所示的指数规律上升到稳态值rw。线圈电流达到rcd所需的时间t′cd可令I=Icd代入式(3-4)后求得,即
T′cd=TLnIW/IW-ICD (s) (3-5)
 △w~△cd
△w~△cd
若令Iw/Icb=Kcb(Kcb称为储备系数),代入式(3-5)得
t′cd=tln (s) (3~6)
以上的推导并未考虑涡流的影响。实际上,当磁通Φ变化时,导磁体内将会产生环绕磁通的感应电流9即所谓涡流。涡流的作用总是使磁通的变化落后于线圈电流的变化,因此,使触动时间变大。在打开位置时,涡流的影响一般不大,可以用一个系数α来考虑它的影响,即
t′cd=αTlnkcb/kcb-1 (s) (3-7)
α一般等于1.1~1.3。
吸合运动时间t′yd
衔铁运动以后,线圈内的电流不再按式(3-4)的指数规律上升。因为,衔铁运动过程中,气隙减小,磁通增大。而磁通的变化将在线圈内感应而产生一个反电势,这个反电势和线圈的自感电势共同阻止线圈电流的增长。此时,由于线圈电感在变化,电路的电压平衡方程将不同于式(3-3),而是
U=iR+Ldi/dt+idl/dt
式(3-8)右边的第二项L器为线圈的自感电势,而第三项f等即为电感变化时的反电势。因此电流的增长规律将低于式(3-4)的指数曲线,随着衔铁运动速度的增加,反电势就越大,两者的差别就这大,电流甚至不再上升反而下降,如图3-11中AB段。B点的位置与衔铁E0运=t速芰有关・速度越大・B点就越低。到达B点,衔铁已闭合而气隙不再变化.线圈电流又近似地按指数规律增长,不过这时线圈的电时间常数已不同于衔铁打开时的电时间常数,因为电感变大了。
电磁铁运动时间的计算是比较麻烦的,因为衔铁在运动过程中除线圈电感变化外,作用于衔铁上的反作用力和电磁吸力都在变化。计算电流变化规律及衔铁的运动时间不仅要研究电和过E变化规律,还要同时研究衔铁的运动规律,也就是说,必须联解下列两个微分方程:
电路方程 u=iR+d/dt (3-9)
运动方程 Fd―Ft=md2/dt2 (3-10)
式中 m――衔铁及其他运动部分的质量;
d2/dt――衔铁的运动丌速度,r为衔铁的行程;
Fd――电磁吸力:
Ff――反作用力:
由于¢和fd是J和的函数,并且是非线性的关系,Ff也与r和于有关,因此很难用
分市F法求解以上E0方程。一般都用近似计算的方法来求解,下面是吸合运动时间tyd的近似计算公式.
电磁继电器的吸合过程和吸合时间,电磁继电器的线圈电路具有一定电感量,在线圈两端加上直流电压[/后,电路中的电J不能跃升至稳态值rw(rw=σ/R,R为线圈电路的电阻值),而是随时间彦按一定的规律上升,如图3-11所示。因此,电磁铁的吸合过程可以分为两个阶段:一个是电流从零开始
上升到触动电流rcd,在这个阶段内衔铁没有运动,所需的时间r′cd称为吸合触动时间。当电流值达到rcd以后,吸力Fd将大于反力F”衔铁开始运动。衔铁运动以后,电流的变化规律变得复杂。从衔铁开始运动到最后达到闭合位置所需的时间hd称为吸合运动时间。因此,电磁继电器的固有吸合时间莎xh包括两部分,即
txh=t′cd+t′yd (3-1)
下面对这两个阶段分别进行一些讨论。
吸合触动时间t′cd
当线圈加上直流电压【厂以后,其电流(或磁通)增长的过渡过程可以由电压平衡方程求得,即
u=ir+d/dt (3-2)
式中 u一线圈电压(V);
i一线圈电流(A);
R――线圈回路总电阻(Ω);
d一线圈总的磁链(Wb);
t一通电时间(s)。
当衔铁处于打开位置时,并且电流又不很大,磁路一般并不饱和,则可以认为线圈电感L为常数,则式(3-2)可改写为
u=iR+Ldi/dt (3-3)
而式(3-3)的解为
i=iw(1-e-t/t) (3-4)
式中 iw一线圈的稳态电流,rw=y/R(A);
T一线圈的电时间常数,T=L/R(s)。
可见1电流按指数曲线上升,如图3-11。假如电流达到fed后衔铁仍保持不动,则电流将按照图中虚线所示的指数规律上升到稳态值rw。线圈电流达到rcd所需的时间t′cd可令I=Icd代入式(3-4)后求得,即
T′cd=TLnIW/IW-ICD (s) (3-5)
 △w~△cd
△w~△cd
若令Iw/Icb=Kcb(Kcb称为储备系数),代入式(3-5)得
t′cd=tln (s) (3~6)
以上的推导并未考虑涡流的影响。实际上,当磁通Φ变化时,导磁体内将会产生环绕磁通的感应电流9即所谓涡流。涡流的作用总是使磁通的变化落后于线圈电流的变化,因此,使触动时间变大。在打开位置时,涡流的影响一般不大,可以用一个系数α来考虑它的影响,即
t′cd=αTlnkcb/kcb-1 (s) (3-7)
α一般等于1.1~1.3。
吸合运动时间t′yd
衔铁运动以后,线圈内的电流不再按式(3-4)的指数规律上升。因为,衔铁运动过程中,气隙减小,磁通增大。而磁通的变化将在线圈内感应而产生一个反电势,这个反电势和线圈的自感电势共同阻止线圈电流的增长。此时,由于线圈电感在变化,电路的电压平衡方程将不同于式(3-3),而是
U=iR+Ldi/dt+idl/dt
式(3-8)右边的第二项L器为线圈的自感电势,而第三项f等即为电感变化时的反电势。因此电流的增长规律将低于式(3-4)的指数曲线,随着衔铁运动速度的增加,反电势就越大,两者的差别就这大,电流甚至不再上升反而下降,如图3-11中AB段。B点的位置与衔铁E0运=t速芰有关・速度越大・B点就越低。到达B点,衔铁已闭合而气隙不再变化.线圈电流又近似地按指数规律增长,不过这时线圈的电时间常数已不同于衔铁打开时的电时间常数,因为电感变大了。
电磁铁运动时间的计算是比较麻烦的,因为衔铁在运动过程中除线圈电感变化外,作用于衔铁上的反作用力和电磁吸力都在变化。计算电流变化规律及衔铁的运动时间不仅要研究电和过E变化规律,还要同时研究衔铁的运动规律,也就是说,必须联解下列两个微分方程:
电路方程 u=iR+d/dt (3-9)
运动方程 Fd―Ft=md2/dt2 (3-10)
式中 m――衔铁及其他运动部分的质量;
d2/dt――衔铁的运动丌速度,r为衔铁的行程;
Fd――电磁吸力:
Ff――反作用力:
由于¢和fd是J和的函数,并且是非线性的关系,Ff也与r和于有关,因此很难用
分市F法求解以上E0方程。一般都用近似计算的方法来求解,下面是吸合运动时间tyd的近似计算公式.



 公网安备44030402000607
公网安备44030402000607





