TPS54540DDAR频率响应的基本概念
发布时间:2019/11/5 23:51:54 访问次数:2148
TPS54540DDAR一般有Cbe>>Cb`c,故值得注意的是,当频率高于5炜或10呢时,混合Ⅱ形模型中的电阻rb`e可以忽略,因而模型中的rbb`成为唯一的电阻,它对管子的高频响应呈现较大的影响。
利用式(4,7,18)及o与卩的关系,可以求出BJT的共基极截止频率fa。
将卩0=gm rlt及式(⒋7,20)代'人上式,则
式中几是o下降为0.707α0时的频率,即BJT的共基极截止频率。
由式(4.7.22)和式(4.7.21a)可得
fa=(1+b0)fb≈fb+yT (4.7.23)
式(4,7.23)说明,BJT的共基极截止频率几远大于共射极截止频率fb,且比特征频率而还高,即BJT的三个频率参数的数量关系为fb<
在了解了频率响应的基本概念、分析方法及BJT的小信号模型之后,下面来分析放大电路的频率响应。
鲞疑箪裟貘 单级共射极放大电路的频率响应现以图4.7.10a所示电路为例,分析其频率响应。
高频响应,在高频范围内,放大电路中的耦合电容、旁路电容的容抗很小,更可视为对交流信号短路,于是可画出图4.7,10a所示电路的高频小信号等效电路,如图4.7.10b所示。现按以下步骤进行分析:
求密勒电容,由于电容Cb`c跨接在输人和输出回路之间,使电路分析较为复杂,为了方便起见,可将Cbc进行单向化处理,即将Cb`c等效变换到输人回路(b′-e之
间)和输出回路中(c-e之间),如图4.7.10c所示。其变换过程如下:
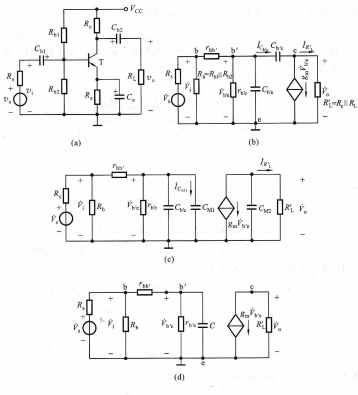
共射电路及其高频小信号等效电路,(a)共射电路原理图 (b)图4.710a的高频小信号等效电路(c)图4,7.10b的密勒等效电路 (d)图4.710c的简化电路
在图4.7.10b中,设A|=y。/7be,则由b′点流人电容Cl)c的电流为
yb`c~yo (1-ui)po`e
由此式可知,只要令图4.7.10c中输入回路的电容
CM1=(1-AI,)(1b`c
使r cM1=rcⅡ,则电容Cbc对输人回路的影响与电容CM1的作用相同。同理,在图4.7.10b的输出回路中,由c点流人Cb`c的电流为
使r cM2=f:bc,则电容Ch`c对输出回路的影响与电容CM2的作用相同。
上述各式中的AI,是图4,7,10b所示电路的yo对ybe的增益,一般有|tg|>>1,由此图可求得且o的表达式如下:
(r cb,c~gm yb`e)R[ [jωCb`e(1-Al)yb`e-gm yb`e]RI
≈-jωCb`cA3RL-gmR
即 1- 1Tiif;k{;;TT (4726a)
因为Cbc很小,通常有RI<o
Ai≈-gmRL (4.7.26b)
将上式代人式(4.7.24b)和式(4.7.25b),即可得Cb`c的密勒等效电容CM1和CM2。显然有CM1>>Cb`c,CM2≈Cbc,CM2的影响可以忽略,于是图4.7.10c可放大电路基础.
TPS54540DDAR一般有Cbe>>Cb`c,故值得注意的是,当频率高于5炜或10呢时,混合Ⅱ形模型中的电阻rb`e可以忽略,因而模型中的rbb`成为唯一的电阻,它对管子的高频响应呈现较大的影响。
利用式(4,7,18)及o与卩的关系,可以求出BJT的共基极截止频率fa。
将卩0=gm rlt及式(⒋7,20)代'人上式,则
式中几是o下降为0.707α0时的频率,即BJT的共基极截止频率。
由式(4.7.22)和式(4.7.21a)可得
fa=(1+b0)fb≈fb+yT (4.7.23)
式(4,7.23)说明,BJT的共基极截止频率几远大于共射极截止频率fb,且比特征频率而还高,即BJT的三个频率参数的数量关系为fb<
在了解了频率响应的基本概念、分析方法及BJT的小信号模型之后,下面来分析放大电路的频率响应。
鲞疑箪裟貘 单级共射极放大电路的频率响应现以图4.7.10a所示电路为例,分析其频率响应。
高频响应,在高频范围内,放大电路中的耦合电容、旁路电容的容抗很小,更可视为对交流信号短路,于是可画出图4.7,10a所示电路的高频小信号等效电路,如图4.7.10b所示。现按以下步骤进行分析:
求密勒电容,由于电容Cb`c跨接在输人和输出回路之间,使电路分析较为复杂,为了方便起见,可将Cbc进行单向化处理,即将Cb`c等效变换到输人回路(b′-e之
间)和输出回路中(c-e之间),如图4.7.10c所示。其变换过程如下:

共射电路及其高频小信号等效电路,(a)共射电路原理图 (b)图4.710a的高频小信号等效电路(c)图4,7.10b的密勒等效电路 (d)图4.710c的简化电路
在图4.7.10b中,设A|=y。/7be,则由b′点流人电容Cl)c的电流为
yb`c~yo (1-ui)po`e
由此式可知,只要令图4.7.10c中输入回路的电容
CM1=(1-AI,)(1b`c
使r cM1=rcⅡ,则电容Cbc对输人回路的影响与电容CM1的作用相同。同理,在图4.7.10b的输出回路中,由c点流人Cb`c的电流为
使r cM2=f:bc,则电容Ch`c对输出回路的影响与电容CM2的作用相同。
上述各式中的AI,是图4,7,10b所示电路的yo对ybe的增益,一般有|tg|>>1,由此图可求得且o的表达式如下:
(r cb,c~gm yb`e)R[ [jωCb`e(1-Al)yb`e-gm yb`e]RI
≈-jωCb`cA3RL-gmR
即 1- 1Tiif;k{;;TT (4726a)
因为Cbc很小,通常有RI<o
Ai≈-gmRL (4.7.26b)
将上式代人式(4.7.24b)和式(4.7.25b),即可得Cb`c的密勒等效电容CM1和CM2。显然有CM1>>Cb`c,CM2≈Cbc,CM2的影响可以忽略,于是图4.7.10c可放大电路基础.



 公网安备44030402000607
公网安备44030402000607





