MC74HC133N测量用互感器的误差
发布时间:2019/11/1 21:16:40 访问次数:1020
MC74HC133Ni1/i2≈w2/w1 (6-7)
因此,在理想情况下,初级电流与次级电流之比和初级、次级两线圈的匝数成反比关系。
测量用互感器的误差及准确度,上节所讨论的理想互感器的变压比或变流比是一个不变的常数,只决定于初级和次级两线圈的匝数。实际上由于互感器中存在着漏磁通,线圈电阻和铁心损耗,因而变压比与变流比并不是一个常数,而出现误差。本节讨论测量用互感器的误差及准确度,并用矢量图对误差进行分析。
测量用互感器的变比误差及相角误差,实际测量用互感器的J1与J2(或电流rl及r2)之比并不是严格保持一个常数Kj(或Kr),而是与互感器的工作状况(即电压和电流的大小,次级负载的大小和特性,以及电流的频率等)及互感器本身的结构和铁心材料等有关。因此,按式(6-1)和式(6-2)求出的数值叽′(或r1′)只是一个近似值,与被测量的实际值y1(或r1)存在一定的误差,通常称该误差为“比值差”,简称“比差”,以7σ(或/f)表示:
yu=u1-u2/u1=kuu2-u1/u1×100% (6-8)
同样
γr=i1-i2/i1=kii2-i1/i1×100% (6・9)
除了比值差之外,还有所谓“相角差”。在理想情况下,电压互感器初、次级电压的矢量应当相差180°的相位角。同样,电流互感器初、次级电流的矢量也应相差180°。但是实际上,它们之间的相位差不可能刚好180°,而是180°+δ,这个δ角就称为互感器的“相角差”(简称“角差”)。δ可以是正的也可以是负的。通常规定:如果矢量况(或r2)・转180°后超前于tr1(或r1),则δ角就算是正的,若滞后于山(或h),则δ角就算是负的。
测量用互感器的矢量图及基本关系式,为测量用互感器的示意图及其矢量图,它与图6-4不同的地方是在主磁通Φ之外,还考虑了初、次级线圈的漏磁通Φ11、Φ12和两线圈的导线电阻u1、u2以及铁心的损耗。
在图6-5(b)中,假定负载为感性的,即r2滞后于巴,而且次级电路中的宝2、I′2、rr2及`r2J2等在绘图时都已乘上W1/″2的换算系数。
在图6-5(b)中,由于考虑到铁心中存在磁滞损耗及涡流损耗,所以rO较Φ导前α角。ri、y2、石、=2分别代表初级线圈和次级线圈的导线电阻及漏电抗。由电工理论可知
e1=rl(rl+`ui)―E1 (6-10)
E2=r2(r2十u4)+y2 (6-11)
电压互感器的工作状态及其误差分析,电压互感器的工作状态的特点是:初级线圈与电源电压直接联接,因此初级电压变动很小,而次级线圈则与大电阻负载(如电压表的附加电阻)相联接,因此,r1与r2都很小,接近于开路状态下工作。
从式(6-10)和式(6-11)两式可知,当r1、r2、幼、∞2不等于零时,虽然E1=4Kfy・″1.m和E2=4Kf灿72Φm还是成立的,但是u≠E1,σ2≠E2,因此,这样就出现了比差u0。又从图6-5(b)和图6-4(b)的比较中可知,在图6-5(b)中,将已72转180°后得到的―已与电压J1不再重合,而是相差一个ε角,因此就出现了相角差a。
随着负载增加,/u和a都会加大,这一点从公式(6-10)、(6-11)和图6-5(b)中是不难理解的。因为当负载增大时,例如并联到电压互感器的电压表(或功率表、电度表的电压线圈)增多时,r2和r1将相应增大,u1和―e1以及y2和它2都将相差更多,这样就使得已、J2间的比差和相角差都增大。
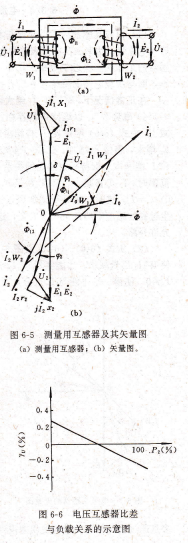
如果设计时将″1与″2的比值选取得就等于额定变压比Κσ,那么,就只有在理想情况下(r1=r2=3=J2=0)才会出现h`=0和a=o。而在实际情况下,即使J2=0(次级电路开路),也会出现[`1>E1=KuE2=Κ山72,从式(6-8)可知,这时将出现负的比差。当r2≠o时,负的比差将随着r2增大而不断增大。为了减少误差,通常将Κε选得大于W1与72的比值,这样就可以调整得到在小负荷时比差为正,而满负荷时为负,如图6-6所示(图中P2为次级电路功率以额定功率的百分数表示)。
由于电压互感器的误差与初级和次级两线圈的电压降有关,因此电压互感器的误差与下列各量都有关线圈电阻r1、r2;漏抗J1、J2;空载(即次级电路开路时)电流r。;F2的数值及相位角物(即次级电路负载的大小及阻抗角);u1的大小及频率等。
为了减小ri和r2,电压互感器铜线的截面选用得J2r2.
MC74HC133Ni1/i2≈w2/w1 (6-7)
因此,在理想情况下,初级电流与次级电流之比和初级、次级两线圈的匝数成反比关系。
测量用互感器的误差及准确度,上节所讨论的理想互感器的变压比或变流比是一个不变的常数,只决定于初级和次级两线圈的匝数。实际上由于互感器中存在着漏磁通,线圈电阻和铁心损耗,因而变压比与变流比并不是一个常数,而出现误差。本节讨论测量用互感器的误差及准确度,并用矢量图对误差进行分析。
测量用互感器的变比误差及相角误差,实际测量用互感器的J1与J2(或电流rl及r2)之比并不是严格保持一个常数Kj(或Kr),而是与互感器的工作状况(即电压和电流的大小,次级负载的大小和特性,以及电流的频率等)及互感器本身的结构和铁心材料等有关。因此,按式(6-1)和式(6-2)求出的数值叽′(或r1′)只是一个近似值,与被测量的实际值y1(或r1)存在一定的误差,通常称该误差为“比值差”,简称“比差”,以7σ(或/f)表示:
yu=u1-u2/u1=kuu2-u1/u1×100% (6-8)
同样
γr=i1-i2/i1=kii2-i1/i1×100% (6・9)
除了比值差之外,还有所谓“相角差”。在理想情况下,电压互感器初、次级电压的矢量应当相差180°的相位角。同样,电流互感器初、次级电流的矢量也应相差180°。但是实际上,它们之间的相位差不可能刚好180°,而是180°+δ,这个δ角就称为互感器的“相角差”(简称“角差”)。δ可以是正的也可以是负的。通常规定:如果矢量况(或r2)・转180°后超前于tr1(或r1),则δ角就算是正的,若滞后于山(或h),则δ角就算是负的。
测量用互感器的矢量图及基本关系式,为测量用互感器的示意图及其矢量图,它与图6-4不同的地方是在主磁通Φ之外,还考虑了初、次级线圈的漏磁通Φ11、Φ12和两线圈的导线电阻u1、u2以及铁心的损耗。
在图6-5(b)中,假定负载为感性的,即r2滞后于巴,而且次级电路中的宝2、I′2、rr2及`r2J2等在绘图时都已乘上W1/″2的换算系数。
在图6-5(b)中,由于考虑到铁心中存在磁滞损耗及涡流损耗,所以rO较Φ导前α角。ri、y2、石、=2分别代表初级线圈和次级线圈的导线电阻及漏电抗。由电工理论可知
e1=rl(rl+`ui)―E1 (6-10)
E2=r2(r2十u4)+y2 (6-11)
电压互感器的工作状态及其误差分析,电压互感器的工作状态的特点是:初级线圈与电源电压直接联接,因此初级电压变动很小,而次级线圈则与大电阻负载(如电压表的附加电阻)相联接,因此,r1与r2都很小,接近于开路状态下工作。
从式(6-10)和式(6-11)两式可知,当r1、r2、幼、∞2不等于零时,虽然E1=4Kfy・″1.m和E2=4Kf灿72Φm还是成立的,但是u≠E1,σ2≠E2,因此,这样就出现了比差u0。又从图6-5(b)和图6-4(b)的比较中可知,在图6-5(b)中,将已72转180°后得到的―已与电压J1不再重合,而是相差一个ε角,因此就出现了相角差a。
随着负载增加,/u和a都会加大,这一点从公式(6-10)、(6-11)和图6-5(b)中是不难理解的。因为当负载增大时,例如并联到电压互感器的电压表(或功率表、电度表的电压线圈)增多时,r2和r1将相应增大,u1和―e1以及y2和它2都将相差更多,这样就使得已、J2间的比差和相角差都增大。

如果设计时将″1与″2的比值选取得就等于额定变压比Κσ,那么,就只有在理想情况下(r1=r2=3=J2=0)才会出现h`=0和a=o。而在实际情况下,即使J2=0(次级电路开路),也会出现[`1>E1=KuE2=Κ山72,从式(6-8)可知,这时将出现负的比差。当r2≠o时,负的比差将随着r2增大而不断增大。为了减少误差,通常将Κε选得大于W1与72的比值,这样就可以调整得到在小负荷时比差为正,而满负荷时为负,如图6-6所示(图中P2为次级电路功率以额定功率的百分数表示)。
由于电压互感器的误差与初级和次级两线圈的电压降有关,因此电压互感器的误差与下列各量都有关线圈电阻r1、r2;漏抗J1、J2;空载(即次级电路开路时)电流r。;F2的数值及相位角物(即次级电路负载的大小及阻抗角);u1的大小及频率等。
为了减小ri和r2,电压互感器铜线的截面选用得J2r2.


 公网安备44030402000607
公网安备44030402000607





