1SMB5935BT3 逻辑仿真和逻辑综合
发布时间:2019/10/10 17:36:47 访问次数:1127
1SMB5935BT3逻辑代数是分析和设计逻辑电路的数学工具。一个逻辑问题可用逻辑函数来描述 ,逻辑函数可用真值表、逻辑表达式、卡诺图和逻辑图表达 ,这4种表达方式各具特点 ,可 根据需要选用。
HDL是一种以文本形式来描述数字系统硬件的结构和行为的语言 ,用它可以表示逻辑电路图、逻辑表达式 ,还 可以表示更复杂的数字逻辑系统所完成的逻辑功能 (即行为 )。 计算机对HDL的处理包括两个方面 :逻辑仿真和逻辑综合。用 HDL设 计数字系统是当今的一种趋势。
逻辑代数
用真值表证明下列恒等式:
(1) (A①B)C)C=a①(B①C)
(2) (A+B)(A+C)=a+BC
(3) a①B=aB+AB
写出三变量的摩根定理表达式,并用真值表验证其正确性。
用逻辑代数定律证明下列等式:
(1) A+AB=A+B
(2) ABC+aBC+AbC=AB+AC
(3) A+ABC+ACD+(C+D)E=a+CD+E
用代数法化简下列各式:
(1) AB(BC+a (2) (A+B)(aB)
AB+ˉ1BC+△(召+△召)
(7) -B+ABC+△C+△B
(9) △BC D+△召I9+BC D+18C召£)+BC (10) △C+1”C+BC+A召C
将下列各式转换成与一或形式:
(1)A①b①C①D
(2)A+B+C+D+C+D+△+D
(3) AC・BD BC・,1B
已知逻辑函数表达式为I=△BC D,ini出实现该式的逻辑电路图,限使用非门
和二输人与非门.
画出实现下列逻辑表达式的逻辑电路图,限使用非闸和二输人与非闸。
(1) L=AB+AC
(2)I=D(A+C)
(3)l=(A+B)(C+D)
已知逻辑函数表达式为I=AB+AC,画出实现该式的逻辑电路图,限使用非门和二输人或非门。
逻辑函数的卡诺图化简法
将下列函数展开为最小项表达式:
(1) l=ACD+BCD+aBCD
(2)l=A(B+C)
(3)l=aB+ABD(B+CD)
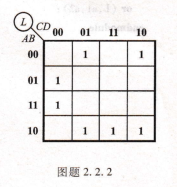
已知函数L(A,B,C,D)的卡诺图如图题2.2.2所不,试写出函数L的最简与或表达式。
用卡诺图法化简下列各式:
(1) ABCd+AbCI)+ab+AD+ABC
(2) (Ab+BD)C+BD(AC)+D(A+B)
00 01 11 10
00
(3) aBCI9+D(BCD) + (a+C) BD+,4(B+ri)
(4)L(a,B,C,D)=∑m(0,2,4,8△0,12) 01
(5)r(A,B,c,D)=∑m(0,1,2,5,6,8,9,10,13,14) 11
(6)E(A找C,D)=∑m(0,2,4,6,9,13)+∑“1, 10,3,5,7,11,15)
(7)I(a,B,C,D)=∑m(0,13,14,15)+∑d(1,2, 3,9,10,11)
1SMB5935BT3逻辑代数是分析和设计逻辑电路的数学工具。一个逻辑问题可用逻辑函数来描述 ,逻辑函数可用真值表、逻辑表达式、卡诺图和逻辑图表达 ,这4种表达方式各具特点 ,可 根据需要选用。
HDL是一种以文本形式来描述数字系统硬件的结构和行为的语言 ,用它可以表示逻辑电路图、逻辑表达式 ,还 可以表示更复杂的数字逻辑系统所完成的逻辑功能 (即行为 )。 计算机对HDL的处理包括两个方面 :逻辑仿真和逻辑综合。用 HDL设 计数字系统是当今的一种趋势。
逻辑代数
用真值表证明下列恒等式:
(1) (A①B)C)C=a①(B①C)
(2) (A+B)(A+C)=a+BC
(3) a①B=aB+AB
写出三变量的摩根定理表达式,并用真值表验证其正确性。
用逻辑代数定律证明下列等式:
(1) A+AB=A+B
(2) ABC+aBC+AbC=AB+AC
(3) A+ABC+ACD+(C+D)E=a+CD+E
用代数法化简下列各式:
(1) AB(BC+a (2) (A+B)(aB)
AB+ˉ1BC+△(召+△召)
(7) -B+ABC+△C+△B
(9) △BC D+△召I9+BC D+18C召£)+BC (10) △C+1”C+BC+A召C
将下列各式转换成与一或形式:
(1)A①b①C①D
(2)A+B+C+D+C+D+△+D
(3) AC・BD BC・,1B
已知逻辑函数表达式为I=△BC D,ini出实现该式的逻辑电路图,限使用非门
和二输人与非门.
画出实现下列逻辑表达式的逻辑电路图,限使用非闸和二输人与非闸。
(1) L=AB+AC
(2)I=D(A+C)
(3)l=(A+B)(C+D)
已知逻辑函数表达式为I=AB+AC,画出实现该式的逻辑电路图,限使用非门和二输人或非门。
逻辑函数的卡诺图化简法
将下列函数展开为最小项表达式:
(1) l=ACD+BCD+aBCD
(2)l=A(B+C)
(3)l=aB+ABD(B+CD)
已知函数L(A,B,C,D)的卡诺图如图题2.2.2所不,试写出函数L的最简与或表达式。
用卡诺图法化简下列各式:
(1) ABCd+AbCI)+ab+AD+ABC
(2) (Ab+BD)C+BD(AC)+D(A+B)
00 01 11 10
00
(3) aBCI9+D(BCD) + (a+C) BD+,4(B+ri)
(4)L(a,B,C,D)=∑m(0,2,4,8△0,12) 01
(5)r(A,B,c,D)=∑m(0,1,2,5,6,8,9,10,13,14) 11
(6)E(A找C,D)=∑m(0,2,4,6,9,13)+∑“1, 10,3,5,7,11,15)
(7)I(a,B,C,D)=∑m(0,13,14,15)+∑d(1,2, 3,9,10,11)




 公网安备44030402000607
公网安备44030402000607





