高精度交流信号振荡器的音频频谱
发布时间:2020/9/19 22:17:28 访问次数:1929
NCO的主要功能部分,以及与完整的直接数字频率合成器的区别,其中包括重构DAC和其相关的AAF。NCO部分可用于测试或仿真DAC,在软件中实现高精度NCO
惠普分析仪,如同应用笔记AN-1323中描述的那样,构建与最出色的模拟振荡器具备同等或更出色的失真性能的高精度交流信号振荡器并不容易,即使是针对音频频谱(直流至20 kHz范围)。
利用嵌入式处理器具有的足够运算精度来执行相位计算(ωt)和正弦函数(sin(ωt))近似计算,从而完整实施软件,这显然有助于最大限度减少量化的不利影响、噪声和由此导致的杂散。
NCO功能模块都会转换成代码行(不是VHDL),从而实现一个满足实时约束的软件版本,以确保实现最小的采样速率和所需的频率带宽。
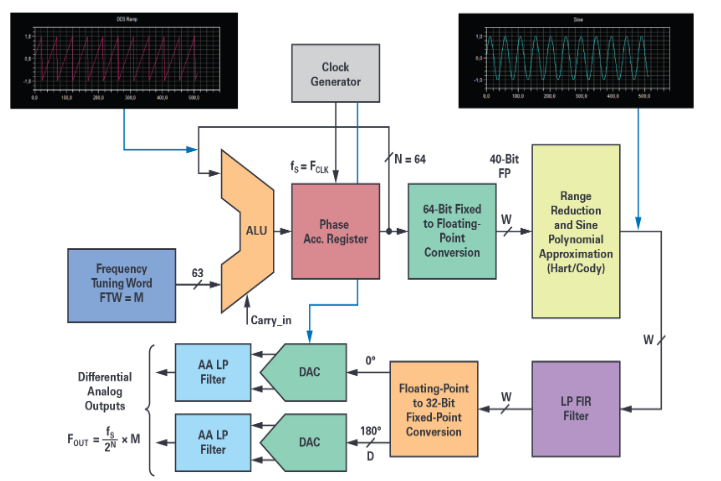
对于相位-正弦幅度转换引擎,完整的LUT方案或任何变化都需要用到太多的存储空间或太多的插值运算来实现完美的正弦一致性。
除了周期性和modulo-2π重复之外,sin(x)函数的对称性可用于进一步缩小近似值范围。鉴于正弦函数在区间[0, 2π]内,关于点x = π不对称,所以能够使用以下关系式:
sin(x+π)+-sin(x)
将范围缩小到[0, π]。采用同样的方式,sin(x)在区间[0, π]内,关于由x = π/2定义的线对称,所以:
sin(x+π/2)+sin(π/2-x)
x在区间[0, π/2]以内,这会进一步缩小角输入近似值的范围。通过进一步缩小参数区间(例如[0, π/4])来提高精度并不是有效方法,因为这需要同时估算正弦和余弦函数的值,如常用三角关系所示:sin(a+b) = sin(a) × cos(b) + cos(a) × sin(b),从生成正交信号这一角度,这有其价值。

ADSP-21000系列应用手册第1卷描述了一个近乎理想的(用于嵌入式系统)正弦近似值函数,该函数基于为第一个ADI DSP浮点处理器编写的幂级数优化,即ADSP-21020,后者基本上属于SHARC核。
这种sin(x)的实现方法依赖于Hart等人4发布、由Cody和Waite5完善、适用于浮点运算的极大极小逼近多项式,以减少舍入错误和避免出现前面提到的取消。
极大极小方法依赖于切比雪夫多项式和雷米兹交换算法来确定所需的最大相对误差的系数。与第七阶泰勒多项式6相比,设置系数的微小变化可能会明显提高极小极大值的精度。为了实现精度与速度的最佳平衡,这个正弦近似值函数的角输入范围应该缩小到[-π/2至+π/2]区间内,且软件程序包含一个有效的范围缩减滤波器,约占总“正弦”子程序执行时间的30%。

(素材:chinaaet.如涉版权请联系删除)
NCO的主要功能部分,以及与完整的直接数字频率合成器的区别,其中包括重构DAC和其相关的AAF。NCO部分可用于测试或仿真DAC,在软件中实现高精度NCO
惠普分析仪,如同应用笔记AN-1323中描述的那样,构建与最出色的模拟振荡器具备同等或更出色的失真性能的高精度交流信号振荡器并不容易,即使是针对音频频谱(直流至20 kHz范围)。
利用嵌入式处理器具有的足够运算精度来执行相位计算(ωt)和正弦函数(sin(ωt))近似计算,从而完整实施软件,这显然有助于最大限度减少量化的不利影响、噪声和由此导致的杂散。
NCO功能模块都会转换成代码行(不是VHDL),从而实现一个满足实时约束的软件版本,以确保实现最小的采样速率和所需的频率带宽。

对于相位-正弦幅度转换引擎,完整的LUT方案或任何变化都需要用到太多的存储空间或太多的插值运算来实现完美的正弦一致性。
除了周期性和modulo-2π重复之外,sin(x)函数的对称性可用于进一步缩小近似值范围。鉴于正弦函数在区间[0, 2π]内,关于点x = π不对称,所以能够使用以下关系式:
sin(x+π)+-sin(x)
将范围缩小到[0, π]。采用同样的方式,sin(x)在区间[0, π]内,关于由x = π/2定义的线对称,所以:
sin(x+π/2)+sin(π/2-x)
x在区间[0, π/2]以内,这会进一步缩小角输入近似值的范围。通过进一步缩小参数区间(例如[0, π/4])来提高精度并不是有效方法,因为这需要同时估算正弦和余弦函数的值,如常用三角关系所示:sin(a+b) = sin(a) × cos(b) + cos(a) × sin(b),从生成正交信号这一角度,这有其价值。

ADSP-21000系列应用手册第1卷描述了一个近乎理想的(用于嵌入式系统)正弦近似值函数,该函数基于为第一个ADI DSP浮点处理器编写的幂级数优化,即ADSP-21020,后者基本上属于SHARC核。
这种sin(x)的实现方法依赖于Hart等人4发布、由Cody和Waite5完善、适用于浮点运算的极大极小逼近多项式,以减少舍入错误和避免出现前面提到的取消。
极大极小方法依赖于切比雪夫多项式和雷米兹交换算法来确定所需的最大相对误差的系数。与第七阶泰勒多项式6相比,设置系数的微小变化可能会明显提高极小极大值的精度。为了实现精度与速度的最佳平衡,这个正弦近似值函数的角输入范围应该缩小到[-π/2至+π/2]区间内,且软件程序包含一个有效的范围缩减滤波器,约占总“正弦”子程序执行时间的30%。

(素材:chinaaet.如涉版权请联系删除)
上一篇:数控振荡器集成带宽线性度性能
上一篇:电磁干扰和链路电源管理的高功效


 公网安备44030402000607
公网安备44030402000607





