VI-22W-EX 周期性和非周期性与模拟波形相同
发布时间:2020/2/8 17:55:56 访问次数:1164
例1.1.4 某通信系统每秒钟传输1544000位(⒈544兆位)数据,求每位数据的时间。
解:按题意,每位数据的时间为1544,周期性和非周期性与模拟波形相同,这两类数字波形。
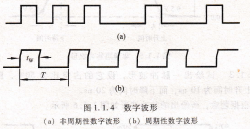
图1.1.4 数字波形,(a)非周期性数字波形 (b)周期性数字波形
周期性数字波形常用周期r和频率r来描述。脉冲波形的脉冲宽度用fw表示,它表示脉冲的作用时间。另一个重要参数是占空比g,它表示脉冲宽度tw占整个周期r的百分数,常用下式来表示(1.1.1),当占空比为50%时,称此时的矩形脉冲为方波,即0和1交替出现并持续占有相同的时间。
例1.1.2 设周期性数字波形的高电平持续6ms,低电平持续10ms,求占空比g。
解:因数字波形的脉冲宽度Jw=6ms,周期r=(6+10)ms=16ms
g=50%・ui×100%*375%
实际数字信号波形,在实际的数字系统中,数字信号并没有那么理想。当它从低电平跳变到高电平,或从高电平跳到低电平时,边沿没有那么陡峭,而要经历一个过渡,过比特率系Bit rme的译称的,位权是相同的。
一般地说,任意十进制数可表示为:
(Ⅳ)D①=∑ui×10n (1.2.1)
式中Ki为基数“10”的第j次幂的系数,它可以是0~9中任何一个数字。如果将式(1.2.1)中的10用字母R来代替,就可以得到任意进制数的表达式:(Ⅳ)R=∑ui×Ru (⒈2.2)
式中Kj是第j次幂的系数,根据基数R的不同,它的取值为0~R-1个不同的数码。例如对于十进制数,R为10,所以Ki的取值为0~9共10个数码。
用数字电路来存储或处理十进制数是不方便的。因为构成数字电路的基本思路是把电路的状态与数码对应起来。而十进制的十个数码要求电路有十个完全不同的状态,这样使得电路很复杂,因此在数字电路中不直接处理十进制数和二进制.
二进制的表示方法,二进制数中,只有0和1两个数码,并且计数规律是“逢二进一”,即1+1=10(读为“壹零”)。必须注意,这里的“10”与十进制数的“10”是完全不同的,它并不代表数“拾”。左边的“1”表示21位数,右边的“0”表示2°位数,也就是10=1×21+0×20。因此,所谓二进制就是以2为基数的计数体制。
根据式(⒈2.2),任意二进制数可表示为(Ⅳ):②=∑KJ×2u (⒈2.3)
式中Kj为基数“2”的第j次幂的系数,它可以是0或者1。这样式(1.2.3)也可以作为二进制数转换为十进制数的转换公式。
例1.2.1 试将二进制数(1010110):转换为十进制数。
解:将每1位二进制数与其位权相乘,然后相加便得相应的十进制数。
(1010110)=1×26+0×25+1×24+Ox23+1×22
标D(Decimal)表示十进制。
标B(Binarv)表示二进制。
深圳市唯有度科技有限公司http://wydkj.51dzw.com/
例1.1.4 某通信系统每秒钟传输1544000位(⒈544兆位)数据,求每位数据的时间。
解:按题意,每位数据的时间为1544,周期性和非周期性与模拟波形相同,这两类数字波形。

图1.1.4 数字波形,(a)非周期性数字波形 (b)周期性数字波形
周期性数字波形常用周期r和频率r来描述。脉冲波形的脉冲宽度用fw表示,它表示脉冲的作用时间。另一个重要参数是占空比g,它表示脉冲宽度tw占整个周期r的百分数,常用下式来表示(1.1.1),当占空比为50%时,称此时的矩形脉冲为方波,即0和1交替出现并持续占有相同的时间。
例1.1.2 设周期性数字波形的高电平持续6ms,低电平持续10ms,求占空比g。
解:因数字波形的脉冲宽度Jw=6ms,周期r=(6+10)ms=16ms
g=50%・ui×100%*375%
实际数字信号波形,在实际的数字系统中,数字信号并没有那么理想。当它从低电平跳变到高电平,或从高电平跳到低电平时,边沿没有那么陡峭,而要经历一个过渡,过比特率系Bit rme的译称的,位权是相同的。
一般地说,任意十进制数可表示为:
(Ⅳ)D①=∑ui×10n (1.2.1)
式中Ki为基数“10”的第j次幂的系数,它可以是0~9中任何一个数字。如果将式(1.2.1)中的10用字母R来代替,就可以得到任意进制数的表达式:(Ⅳ)R=∑ui×Ru (⒈2.2)
式中Kj是第j次幂的系数,根据基数R的不同,它的取值为0~R-1个不同的数码。例如对于十进制数,R为10,所以Ki的取值为0~9共10个数码。
用数字电路来存储或处理十进制数是不方便的。因为构成数字电路的基本思路是把电路的状态与数码对应起来。而十进制的十个数码要求电路有十个完全不同的状态,这样使得电路很复杂,因此在数字电路中不直接处理十进制数和二进制.
二进制的表示方法,二进制数中,只有0和1两个数码,并且计数规律是“逢二进一”,即1+1=10(读为“壹零”)。必须注意,这里的“10”与十进制数的“10”是完全不同的,它并不代表数“拾”。左边的“1”表示21位数,右边的“0”表示2°位数,也就是10=1×21+0×20。因此,所谓二进制就是以2为基数的计数体制。
根据式(⒈2.2),任意二进制数可表示为(Ⅳ):②=∑KJ×2u (⒈2.3)
式中Kj为基数“2”的第j次幂的系数,它可以是0或者1。这样式(1.2.3)也可以作为二进制数转换为十进制数的转换公式。
例1.2.1 试将二进制数(1010110):转换为十进制数。
解:将每1位二进制数与其位权相乘,然后相加便得相应的十进制数。
(1010110)=1×26+0×25+1×24+Ox23+1×22
标D(Decimal)表示十进制。
标B(Binarv)表示二进制。
深圳市唯有度科技有限公司http://wydkj.51dzw.com/


 公网安备44030402000607
公网安备44030402000607





