WP4C1 计数器清零端
发布时间:2019/10/25 17:36:30 访问次数:957
WP4C1出端Co。当计数到050403Q2Q1q0=111011,即盯=60时,Co=1,将其反相后接入使能端,就可以保持在M=60状态。控制单元发出的s,r信号是高电平有效,所以经反相后接至计数器清零端,具体电路可使用中规模芯片自行系统设计.
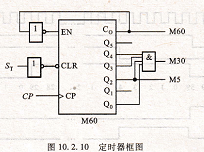
出是在Q1QO驱动下的六个信号灯,各状态与信号灯的关系如表
10.2.2所示,因此,得到灯光信号与控制单元状态变量的关系为
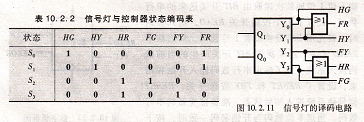
hg=01QO hy=0lqo hR=Q1
FG=Q1qo Fy=O10O FR=O1
实现上述关系的译码电路如图10.2.11所示。
信号灯与控制器状态编,图10.2.11 信号灯的译码电路
D触发器选用74HC74,多路选择器选用74HC153,译码器选用74HC139外加反相器(74HC04)构成输出高电平有效电路,计数器选用74HC163,就可构成系统电路。系统逻辑图略。系统工作波形如图10.2.12所示。
例10.2.2 设计一个8位串行数字密码锁,该锁只有当依次收到的8位串行码与规定的二进制数码一致时,才能被打开。
解:设计过程如下:
明确系统的功能,进行逻辑抽象式中AC和CD两项都是由与(逻辑乘)运算把变量连接起来的,故称为与项(乘积项),然后由或运算将这两个与项连接起来,这种类型的表达式称为与一或逻辑表达式,或称为逻辑函数表达式的“积之和”形式。
在若干个逻辑关系相同的与一或表达式中,将其中包含的与项数最少,且每个与项中变量数最少的表达式称为最简与一或表达式。
一个与一或表达式易于转换为其他类型的函数式,例如,上面的与一或表达式经过变换,可以得到其与非一与非表达式、或一与表达式、或非一或非表达式以及与一或一非表达式等。例如:
乙=AC+C~D 与一或表达式
=AC・CD 与非一与非表达式
=(A+C)(C+D) 或一与表达式
=(A+C)+(C+£)) 或非一或非表达式
=AC+CD 与一或非表达式
以上五个式子是同一函数不同形式的最简表达式。
逻辑函数化简就是要消去与一或表达式中多余的乘积项和每个乘积项中多余的变量,以得到逻辑函数的最简与一或表达式。有了最简与一或表达式以后,再用公式变换就可以得到其他类型的函数式,所以下面着重讨论与一或表达式的化简。
逻辑函数的化简方法,常用的有代数法和卡诺图法(2.2节介绍)等。代数法就是运用逻辑代数的基本定律和恒等式对逻辑函数进行化简,这种方法需要一些技巧,没有固定的步骤。下面是经常使用的方法:
并项法,利用A+A=1的公式,将两项合并成一项,并消去一个变量。
例2.1.3 试用并项法化简下列与一或逻辑函数表达式。
L1=A BC+ABC
l2=A(BC+BC)+处(BC+BC)
解: L1=AB(C+C)=AB
L2 =ABC+ABC+AB C+A BC
=AB(C+C)+AB(C+C)
=A(B+B)=A
WP4C1出端Co。当计数到050403Q2Q1q0=111011,即盯=60时,Co=1,将其反相后接入使能端,就可以保持在M=60状态。控制单元发出的s,r信号是高电平有效,所以经反相后接至计数器清零端,具体电路可使用中规模芯片自行系统设计.

出是在Q1QO驱动下的六个信号灯,各状态与信号灯的关系如表
10.2.2所示,因此,得到灯光信号与控制单元状态变量的关系为
hg=01QO hy=0lqo hR=Q1
FG=Q1qo Fy=O10O FR=O1
实现上述关系的译码电路如图10.2.11所示。
信号灯与控制器状态编,图10.2.11 信号灯的译码电路
D触发器选用74HC74,多路选择器选用74HC153,译码器选用74HC139外加反相器(74HC04)构成输出高电平有效电路,计数器选用74HC163,就可构成系统电路。系统逻辑图略。系统工作波形如图10.2.12所示。

例10.2.2 设计一个8位串行数字密码锁,该锁只有当依次收到的8位串行码与规定的二进制数码一致时,才能被打开。
解:设计过程如下:
明确系统的功能,进行逻辑抽象式中AC和CD两项都是由与(逻辑乘)运算把变量连接起来的,故称为与项(乘积项),然后由或运算将这两个与项连接起来,这种类型的表达式称为与一或逻辑表达式,或称为逻辑函数表达式的“积之和”形式。
在若干个逻辑关系相同的与一或表达式中,将其中包含的与项数最少,且每个与项中变量数最少的表达式称为最简与一或表达式。
一个与一或表达式易于转换为其他类型的函数式,例如,上面的与一或表达式经过变换,可以得到其与非一与非表达式、或一与表达式、或非一或非表达式以及与一或一非表达式等。例如:
乙=AC+C~D 与一或表达式
=AC・CD 与非一与非表达式
=(A+C)(C+D) 或一与表达式
=(A+C)+(C+£)) 或非一或非表达式
=AC+CD 与一或非表达式
以上五个式子是同一函数不同形式的最简表达式。
逻辑函数化简就是要消去与一或表达式中多余的乘积项和每个乘积项中多余的变量,以得到逻辑函数的最简与一或表达式。有了最简与一或表达式以后,再用公式变换就可以得到其他类型的函数式,所以下面着重讨论与一或表达式的化简。
逻辑函数的化简方法,常用的有代数法和卡诺图法(2.2节介绍)等。代数法就是运用逻辑代数的基本定律和恒等式对逻辑函数进行化简,这种方法需要一些技巧,没有固定的步骤。下面是经常使用的方法:
并项法,利用A+A=1的公式,将两项合并成一项,并消去一个变量。
例2.1.3 试用并项法化简下列与一或逻辑函数表达式。
L1=A BC+ABC
l2=A(BC+BC)+处(BC+BC)
解: L1=AB(C+C)=AB
L2 =ABC+ABC+AB C+A BC
=AB(C+C)+AB(C+C)
=A(B+B)=A
上一篇:VI-21W-EY 数字密码锁



 公网安备44030402000607
公网安备44030402000607





