SLA24C04DP 滤波电路的幅频衰减
发布时间:2020/2/11 20:43:05 访问次数:1966
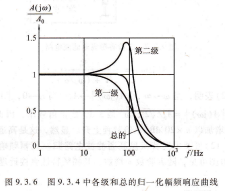
SLA24C04DP指出AuF1=1.152,Al、F2=2.235,由此可求出01=1/(3-uF1)≈0.541,G=1/(3-A n2)≈⒈31。由图可见,由于Q1<0.707,第一级曲线没有峰值;第二级由于02)0,707,在∫=100 Hz附近出现峰值。而总的增益是各级增益的乘积(当各级增益用dB表示时,则是各级增益的相加),因此总的幅频响应曲线消除了峰值,使四阶电路幅频响应的平坦部分得到了扩展,体现了巴特沃思低通滤波电路的特点。
u/(jω)=15Hz
图9.3.6 图9.3.4中各级和总的归化幅频响应曲线
9.3.2 有源高通滤波电路,二阶高通滤波电路
由4.7.1节讨论已知,如果将Rc低通电路中的R和C的位置互换,就可得到RC高通电路。同理,如果将图9.3.1所示二阶有源低通滤波电路中的R和C位置互换,则可得到有源高通滤波电路,如图9.3.7所示。
由于二阶高通滤波电路与二阶低通滤波电路在电路结构上存在对偶关系,它们的传递函数和幅频响应也存在对偶关系。由图9.3,7可导出其传递
函数为A(s)=iOs
s2+ (ut,(u/0)s+ω
s2+ (ωc/O)-s+ωc
第一级、高阶有源滤波电路少,幅频增益以80 dB/十倍频程下降,此外,由于受运放增益带宽积为有限值的影响,由图还可看到,r在1 MHz以上时(此时由于运放的增益带宽积不够),高通滤波电器的幅频响应有所下降。
201g|u|/d=160Hz
图9.3.9 四阶巴特沃思高通滤波电路幅频响应曲线

对照图9.3,5和图9,3.9可以看出,四阶低通滤波电路和四阶高通滤波电路的幅频特性也具有对偶关系,以F=u=100 Hz为对称轴,四阶低通滤波电路的201g(当F<j时)随y升高而增大。
有源带通滤波电路,电路组成原理,由图9.3.10b所示带通滤波电路的幅频响应与高通、低通滤波电路的幅频响应进行比较,不难发现低通与高通滤波电路相串联如图9,3.10a所示,可以构成带通滤波电路,条仵是低通滤波电路的截止角频率ωH大于高通滤波电路的截止角频率ω1.,两者覆盖的通带就提供了一个带通响应。
设计举例,例9.3.2 试设计一带通滤波电路。要求:(1)信号通过频率范围F在100 Hz至10 kHz之间;(2)滤波电路在1 kHz的幅频响应必须在±1 dB范围内,而在100 Hz至10 kHz滤波电路的幅频衰减应当在1 kHz时值的±3 dB范围内;(3)在10 Hz时幅频衰减应为26 dB,而在100 kHz时幅频衰减应至少为16 dB,电路方案选择,高阶有源滤波电路.
深圳市唯有度科技有限公司http://wydkj.51dzw.com/
SLA24C04DP指出AuF1=1.152,Al、F2=2.235,由此可求出01=1/(3-uF1)≈0.541,G=1/(3-A n2)≈⒈31。由图可见,由于Q1<0.707,第一级曲线没有峰值;第二级由于02)0,707,在∫=100 Hz附近出现峰值。而总的增益是各级增益的乘积(当各级增益用dB表示时,则是各级增益的相加),因此总的幅频响应曲线消除了峰值,使四阶电路幅频响应的平坦部分得到了扩展,体现了巴特沃思低通滤波电路的特点。
u/(jω)=15Hz
图9.3.6 图9.3.4中各级和总的归化幅频响应曲线

9.3.2 有源高通滤波电路,二阶高通滤波电路
由4.7.1节讨论已知,如果将Rc低通电路中的R和C的位置互换,就可得到RC高通电路。同理,如果将图9.3.1所示二阶有源低通滤波电路中的R和C位置互换,则可得到有源高通滤波电路,如图9.3.7所示。
由于二阶高通滤波电路与二阶低通滤波电路在电路结构上存在对偶关系,它们的传递函数和幅频响应也存在对偶关系。由图9.3,7可导出其传递
函数为A(s)=iOs
s2+ (ut,(u/0)s+ω
s2+ (ωc/O)-s+ωc
第一级、高阶有源滤波电路少,幅频增益以80 dB/十倍频程下降,此外,由于受运放增益带宽积为有限值的影响,由图还可看到,r在1 MHz以上时(此时由于运放的增益带宽积不够),高通滤波电器的幅频响应有所下降。
201g|u|/d=160Hz
图9.3.9 四阶巴特沃思高通滤波电路幅频响应曲线

对照图9.3,5和图9,3.9可以看出,四阶低通滤波电路和四阶高通滤波电路的幅频特性也具有对偶关系,以F=u=100 Hz为对称轴,四阶低通滤波电路的201g(当F<j时)随y升高而增大。
有源带通滤波电路,电路组成原理,由图9.3.10b所示带通滤波电路的幅频响应与高通、低通滤波电路的幅频响应进行比较,不难发现低通与高通滤波电路相串联如图9,3.10a所示,可以构成带通滤波电路,条仵是低通滤波电路的截止角频率ωH大于高通滤波电路的截止角频率ω1.,两者覆盖的通带就提供了一个带通响应。
设计举例,例9.3.2 试设计一带通滤波电路。要求:(1)信号通过频率范围F在100 Hz至10 kHz之间;(2)滤波电路在1 kHz的幅频响应必须在±1 dB范围内,而在100 Hz至10 kHz滤波电路的幅频衰减应当在1 kHz时值的±3 dB范围内;(3)在10 Hz时幅频衰减应为26 dB,而在100 kHz时幅频衰减应至少为16 dB,电路方案选择,高阶有源滤波电路.
深圳市唯有度科技有限公司http://wydkj.51dzw.com/



 公网安备44030402000607
公网安备44030402000607





