MCM6726BWJ12激励放大器方块图
发布时间:2019/11/3 17:39:20 访问次数:1609
MCM6726BWJ12激励线圈中产生微弱的随机脉冲。该阶跃信号通过激振线圈时引起磁场改变,形成脉冲力,从而引起筒壁变形,使圆筒以低振幅的谐振频率振动。筒壁位移被拾振线圈感受,从而在拾振线圈中产生感应电势。显然,如果外部不继续供能量给激振的机械系统,则由于阻尼作用,振荡是逐渐衰减的。为此,通过外电路使拾振线圈输出的感应电势经放大后再反馈到激振线圈,产生激振。于是,圆筒迅速进入大幅度谐振状态,并以一定的振型继续振荡。
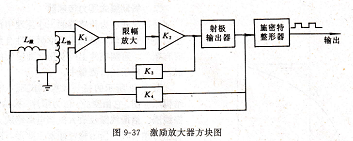
当被测压力通入圆筒内腔时,由于被测压力的作用,沿轴向和径向被张紧的圆筒的刚度发生变化,从而改变了筒的谐振频率。拾振线圈一方面直接检测出随压力而变的振动频率的增量,通过数字电路显示出来;另一方面又不断地把感应电势反馈到激振线圈产生激励力,使圆筒维持振动。由于最大激励电压被限制在一个固定值(5V左右)。因此,圆筒壁最大变形量也决不会超过某个固定值。实际上,筒的径向最大振动只有3u拭左右,轴向是1um左右。
振动频率与压力的关系,根据材料力学可知,振动频率与压力的关系一般可表示为
P=a(rP―fo)+3(FP―fo)2+c(rP一fo)3 (9~17)
式中 P―被测压力;
a、b、c―系数。可由实验求得,一般系数c很小,故c(rP―几)3项可忽略不计;
rP―与压力P相对应的振动频率;
FO―筒的初始频率,即零压力(P=0)频率。
当系数a、b满足一定条件时,可得到传感器输出频率与压力的关系为
fp=fo.1+bp (9-18)
式中 P--待测压力
B一压差灵敏度系数。它与圆筒材料性质及物理尺寸有关。当压力通入圆筒内腔时取正值,通入外腔时取负值。
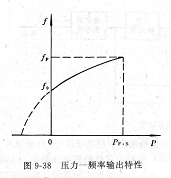
由式(9-18)可明显看出,压力与频率近似成抛物线关系,如图9-38所示。当压力为零时,其频率为筒的初始固有频率几。
振筒式压力传感器的精度比一般模拟量输出压力传感器高1~2个数量级,工作极其可靠,长期稳定性好,尤其适宜于比较恶劣环境条件下的测试。由于这一系列独特的优点,近年来超音速飞机上装各了振筒式压力传感器,获得飞行中的正确高度和速度,经计算机直接解算可进行大气数据参数测量。同时,它还可作压力测试标准仪器,也可用来代替无汞压力计。
振动膜式压力传感器的工作原理与振动筒式压力传感器相似,是利用圆形恒弹性合金膜片的固有频率,可随膜片上所受压力而变化的原理构成,广泛用于压力测量中。
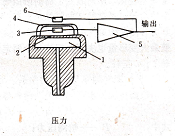
是一种振膜式压力传感器的结构原理图。它由空腔、压力膜片、振动膜片、激振线圈、拾振线圈及放大振荡电路组成。在空腔受压力作用时,压力膜片即发生变形,在压力膜片的支架上装有一振膜。由压力所引起的压力膜压力―频率输出特性 片变形以后,使支架角度改变并张紧振动膜片使其刚度变化。膜片的振动频率取决于振膜的刚度、压力膜片和支架的刚度。在振动膜片的两侧分别放置激励线圈和拾振线圈。当电路接通时,激励线圈中流过交变电流而产生一激励信号使膜片产生振动,通过拾振线圈及振荡放大电路输出后,又正反馈给激励线圈,以维持振膜的振动。
另一种振膜式压力传感器的结构示意图如图9-40所示。它是利用两个压电元件代替激励线圈和拾振线圈。当膜片受压力作用而变形时,其刚度发生变化,膜片的固有频率也随之改变。起拾振作用的压电元件利用顺压电效应,将检测到的信号送入放大器,经放大的信号又正反馈到起激励作用中压电元件,该压电元件利用逆压电效应对晶体施加交变电场,晶体本身将产生机械变形而产生振动以维持振膜的振动。
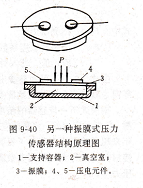
差动电感式压差传感器,振膜式压力传感器结构原理图,1一空腔;2一压力膜片;3一拾振线圈;4一振膜;5一振荡放大电路;6一振动发生器。
电感式传感器原理,电感式传感器属于变磁阻式传感器中的一类。它实质上
就是一个带铁心的线圈,它的工作原理基于机械量变化会引起线圈磁回路磁阻的变化,从而导致电感量的变化这一物理现象。
最简单的电感传感器原理图。铁心和衔铁均由导磁材料如硅钢片或坡莫合金制成,可以是整体的或者叠片的,衔铁和铁心之间有空气隙。当衔铁移动时,气隙大小a的改变使得磁路磁阻发生了变化,从而引起线圈电感的变化。因此,这种电感量的变化是与衔铁位置(即气隙大小)相对应的。只要能测出电感量的变化就能判定衔铁位移量的大小,这就是电感式传感器的基本原理,它与交流电磁铁十分相似。
再观察表6.3.7,又出现状态d和F是等价的,状态F亦可去除,代之以d。于是,得到表6,3,8所示的状态表。检查该表,已不存在等价状态,因此是最简状态表。根据表6.3.8画出的状态图如图6,3.11所示。
表6,3.8 例6.3.3的最简状态表,上述状态化简过程将原有的7个状态化简为5个,而输人一输出特性与原始状态表和原始状态图完全相同。
状态分配,表6.3.8中列出5个状态,最简单的状态分配是使用自然二进制码,取
进制计数序列的前5个连续编码,如6.3,9中的状态分配方案1。结合6.3.11可以看出,这种二进制编码值递增顺序基本上与相应的状态转换顺一致。对于较简单的时序电路,按这状态分配方案构成的时序电路,其组电路将可能相对简单一些。
表6,3.9中所列方案2为格雷码方案。如果状态图所示的主要状态转换顺序是简单的从o到e,那么它从一个状化简后的状态图电路的可靠性。
虽然这将使用较多的触,有些国外文献称之为“0ne~Hot Encoding”,国内某些文献直译为“1位热码编码”。
态转换到下状态,使用发器,但它的编码方式非常简单,可有效地简化组合电路,并且还可以提高工作可靠性和工作速度。在大规模可编程逻辑器件,例如FPGA(见7.4节)中,触发器数量较多而门逻辑相对较少,“一对一”的编码方案有时反而更有利于提高器件资源的利用率。
MCM6726BWJ12激励线圈中产生微弱的随机脉冲。该阶跃信号通过激振线圈时引起磁场改变,形成脉冲力,从而引起筒壁变形,使圆筒以低振幅的谐振频率振动。筒壁位移被拾振线圈感受,从而在拾振线圈中产生感应电势。显然,如果外部不继续供能量给激振的机械系统,则由于阻尼作用,振荡是逐渐衰减的。为此,通过外电路使拾振线圈输出的感应电势经放大后再反馈到激振线圈,产生激振。于是,圆筒迅速进入大幅度谐振状态,并以一定的振型继续振荡。

当被测压力通入圆筒内腔时,由于被测压力的作用,沿轴向和径向被张紧的圆筒的刚度发生变化,从而改变了筒的谐振频率。拾振线圈一方面直接检测出随压力而变的振动频率的增量,通过数字电路显示出来;另一方面又不断地把感应电势反馈到激振线圈产生激励力,使圆筒维持振动。由于最大激励电压被限制在一个固定值(5V左右)。因此,圆筒壁最大变形量也决不会超过某个固定值。实际上,筒的径向最大振动只有3u拭左右,轴向是1um左右。
振动频率与压力的关系,根据材料力学可知,振动频率与压力的关系一般可表示为
P=a(rP―fo)+3(FP―fo)2+c(rP一fo)3 (9~17)
式中 P―被测压力;
a、b、c―系数。可由实验求得,一般系数c很小,故c(rP―几)3项可忽略不计;
rP―与压力P相对应的振动频率;
FO―筒的初始频率,即零压力(P=0)频率。
当系数a、b满足一定条件时,可得到传感器输出频率与压力的关系为
fp=fo.1+bp (9-18)
式中 P--待测压力
B一压差灵敏度系数。它与圆筒材料性质及物理尺寸有关。当压力通入圆筒内腔时取正值,通入外腔时取负值。
由式(9-18)可明显看出,压力与频率近似成抛物线关系,如图9-38所示。当压力为零时,其频率为筒的初始固有频率几。

振筒式压力传感器的精度比一般模拟量输出压力传感器高1~2个数量级,工作极其可靠,长期稳定性好,尤其适宜于比较恶劣环境条件下的测试。由于这一系列独特的优点,近年来超音速飞机上装各了振筒式压力传感器,获得飞行中的正确高度和速度,经计算机直接解算可进行大气数据参数测量。同时,它还可作压力测试标准仪器,也可用来代替无汞压力计。
振动膜式压力传感器的工作原理与振动筒式压力传感器相似,是利用圆形恒弹性合金膜片的固有频率,可随膜片上所受压力而变化的原理构成,广泛用于压力测量中。
是一种振膜式压力传感器的结构原理图。它由空腔、压力膜片、振动膜片、激振线圈、拾振线圈及放大振荡电路组成。在空腔受压力作用时,压力膜片即发生变形,在压力膜片的支架上装有一振膜。由压力所引起的压力膜压力―频率输出特性 片变形以后,使支架角度改变并张紧振动膜片使其刚度变化。膜片的振动频率取决于振膜的刚度、压力膜片和支架的刚度。在振动膜片的两侧分别放置激励线圈和拾振线圈。当电路接通时,激励线圈中流过交变电流而产生一激励信号使膜片产生振动,通过拾振线圈及振荡放大电路输出后,又正反馈给激励线圈,以维持振膜的振动。

另一种振膜式压力传感器的结构示意图如图9-40所示。它是利用两个压电元件代替激励线圈和拾振线圈。当膜片受压力作用而变形时,其刚度发生变化,膜片的固有频率也随之改变。起拾振作用的压电元件利用顺压电效应,将检测到的信号送入放大器,经放大的信号又正反馈到起激励作用中压电元件,该压电元件利用逆压电效应对晶体施加交变电场,晶体本身将产生机械变形而产生振动以维持振膜的振动。

差动电感式压差传感器,振膜式压力传感器结构原理图,1一空腔;2一压力膜片;3一拾振线圈;4一振膜;5一振荡放大电路;6一振动发生器。
电感式传感器原理,电感式传感器属于变磁阻式传感器中的一类。它实质上
就是一个带铁心的线圈,它的工作原理基于机械量变化会引起线圈磁回路磁阻的变化,从而导致电感量的变化这一物理现象。
最简单的电感传感器原理图。铁心和衔铁均由导磁材料如硅钢片或坡莫合金制成,可以是整体的或者叠片的,衔铁和铁心之间有空气隙。当衔铁移动时,气隙大小a的改变使得磁路磁阻发生了变化,从而引起线圈电感的变化。因此,这种电感量的变化是与衔铁位置(即气隙大小)相对应的。只要能测出电感量的变化就能判定衔铁位移量的大小,这就是电感式传感器的基本原理,它与交流电磁铁十分相似。
再观察表6.3.7,又出现状态d和F是等价的,状态F亦可去除,代之以d。于是,得到表6,3,8所示的状态表。检查该表,已不存在等价状态,因此是最简状态表。根据表6.3.8画出的状态图如图6,3.11所示。
表6,3.8 例6.3.3的最简状态表,上述状态化简过程将原有的7个状态化简为5个,而输人一输出特性与原始状态表和原始状态图完全相同。
状态分配,表6.3.8中列出5个状态,最简单的状态分配是使用自然二进制码,取
进制计数序列的前5个连续编码,如6.3,9中的状态分配方案1。结合6.3.11可以看出,这种二进制编码值递增顺序基本上与相应的状态转换顺一致。对于较简单的时序电路,按这状态分配方案构成的时序电路,其组电路将可能相对简单一些。
表6,3.9中所列方案2为格雷码方案。如果状态图所示的主要状态转换顺序是简单的从o到e,那么它从一个状化简后的状态图电路的可靠性。
虽然这将使用较多的触,有些国外文献称之为“0ne~Hot Encoding”,国内某些文献直译为“1位热码编码”。
态转换到下状态,使用发器,但它的编码方式非常简单,可有效地简化组合电路,并且还可以提高工作可靠性和工作速度。在大规模可编程逻辑器件,例如FPGA(见7.4节)中,触发器数量较多而门逻辑相对较少,“一对一”的编码方案有时反而更有利于提高器件资源的利用率。



 公网安备44030402000607
公网安备44030402000607





