VY22256A极面S1的磁通
发布时间:2019/10/28 13:24:46 访问次数:668
VY22256A在一部分极面上装短路环如图1-25所示,即可达到磁通的分相作用,因此短路环这时也称为分磁环。
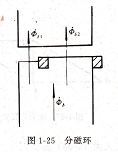
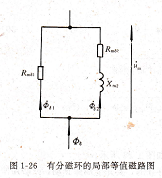
我们知道,在铁心上套一个短路线圈,相当于在磁路参数中有一个磁抗。因此,被分磁环包围的部分就是一个有磁抗的分支磁路,而未被包围的部分则是一个只有气隙磁阻的分支磁路,其等值磁路图如图1-26所示。
um=Φδ1Rmδ1=Φδ2(Rmδ2ˉˉ+`Xm2)
Φdt
Φd2
Rmδ2+Xm2t
¢==arctg.It
图1-25 分磁环而Rmδ2rd1==tt(y―CosZb,有分磁环的局部等值磁路图 vdd=Φδ1msint
u2=Φδ2msin(‘t)
份1为通过没有被环包围的那部分极面S1的磁通,Φδ2为通过被短路环所包围的那部分极面s2的磁通。
加装短路环后电磁铁的吸力,Φδ1和Φδ2在衔铁上产生的吸力分别为(根据式(1-32))作用在衔铁上总的吸力为Fd=Fd1+Fd2=Fdp1+Fdp2
Fdp1cos2‘yt―Fdp2cos(2‘vu一2砂) (N)(1-38)
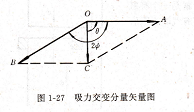
式(1-38)中后两项是同频率的交变分量,其矢量图如图1-27所示。
图中0⒕表示Fd1的交变分量,OB表示Fd2的交变分量,oC是两者的合成矢量。则二交变分量合成后为
Fdmcos2u+Fdp2c°s(2t~2¢)
F:pl+F:p2+2Fdp1Fdp2cos2h
×cos(2t一d)
图1-27 吸力交变分量矢量图召
Fd=Fdp1+Fdp2
F:p1+F:p2+2Fdp1Fdp2cos2tcos(2mt―h)
(1-39)
由式.(1-38)可见,合成吸力最大值为
F:p1+F:p2+2Fdp1Fdp2cos2t (N)
F:pl+F:p2+2Fdp1Fdp2cos2t (N)
最小值大于反力,即Fdmin)>FF
Φδ1(ωf)、Φδ2(‘记9t),Fd1(α,t),Fd2(t)和F2(t)的关系曲线如图1-28示。
必须指出,即使满足式(1-40),吸力的脉动还是存在的,要完全消除脉动,则必须使式(1-39)中的交变分量等于零,即Fgp1+F:p2+2Fdp1Fdp2cos2矽=0要满足上述条件,应使(1)Fdp1=Fdp2;
即而√2仍″Rmδ1 ’R缶δ2+X备2,所以s1S2Φ2m=u代入式(1-38)即(N)Fdmax=Fdp1+Fdp2最小值为Fdmin=Fap1+Fdp2Φ?
作用在衔铁上总的吸力为Fd=Fd1+Fd2=Fdp1+Fdp2ˉFdp1cos2‘妙莎―Fdp2cos(2‘v矽一2砂) (N)(1-38)
式(1-38)中后两项是同频率的交变分量,其矢量图如图1-27所示。
图中0⒕表示Fd1的交变分量,OB表示Fd2的交变分量,oC是两者的合成矢量。则二交变分量合成后为Fdmcos2弼+Fdp2c°s(2耐~2¢)
Fipl+F:p2+2Fdp1Fdp2cos2矽
×cos(2弼一矽)
吸力交变分量矢量图
Fd=Fdp1+Fdp2
F:p1+F:p2+2Fdp1Fdp2cos2砂cos(2m莎―矽)(1-39)
由式.(1-38)可见,合成吸力最大值为
F:p1+F:p2+2Fdp1Fdp2cos2矽 (N)
F:pl+F:p2+2Fdp1Fdp2cos2矽 (N)
最小值大于反力,即Fdmin)>FF
Φδ1(ωf)、Φδ2(‘记9莎),Fd1(α,莎),Fd2(弼)和F2(耐)的关系曲线如图1-28示。
必须指出,即使满足式(1-40),吸力的脉动还是存在的,要完全消除脉动,则必须使式(1-39)中的交变分量等于零,即Fgp1+F:p2+2Fdp1Fdp2cos2矽=0,要满足上述条件.
VY22256A在一部分极面上装短路环如图1-25所示,即可达到磁通的分相作用,因此短路环这时也称为分磁环。

我们知道,在铁心上套一个短路线圈,相当于在磁路参数中有一个磁抗。因此,被分磁环包围的部分就是一个有磁抗的分支磁路,而未被包围的部分则是一个只有气隙磁阻的分支磁路,其等值磁路图如图1-26所示。

um=Φδ1Rmδ1=Φδ2(Rmδ2ˉˉ+`Xm2)
Φdt
Φd2
Rmδ2+Xm2t
¢==arctg.It
图1-25 分磁环而Rmδ2rd1==tt(y―CosZb,有分磁环的局部等值磁路图 vdd=Φδ1msint
u2=Φδ2msin(‘t)
份1为通过没有被环包围的那部分极面S1的磁通,Φδ2为通过被短路环所包围的那部分极面s2的磁通。
加装短路环后电磁铁的吸力,Φδ1和Φδ2在衔铁上产生的吸力分别为(根据式(1-32))作用在衔铁上总的吸力为Fd=Fd1+Fd2=Fdp1+Fdp2
Fdp1cos2‘yt―Fdp2cos(2‘vu一2砂) (N)(1-38)
式(1-38)中后两项是同频率的交变分量,其矢量图如图1-27所示。
图中0⒕表示Fd1的交变分量,OB表示Fd2的交变分量,oC是两者的合成矢量。则二交变分量合成后为
Fdmcos2u+Fdp2c°s(2t~2¢)
F:pl+F:p2+2Fdp1Fdp2cos2h
×cos(2t一d)
图1-27 吸力交变分量矢量图召
Fd=Fdp1+Fdp2
F:p1+F:p2+2Fdp1Fdp2cos2tcos(2mt―h)
(1-39)
由式.(1-38)可见,合成吸力最大值为
F:p1+F:p2+2Fdp1Fdp2cos2t (N)
F:pl+F:p2+2Fdp1Fdp2cos2t (N)
最小值大于反力,即Fdmin)>FF
Φδ1(ωf)、Φδ2(‘记9t),Fd1(α,t),Fd2(t)和F2(t)的关系曲线如图1-28示。
必须指出,即使满足式(1-40),吸力的脉动还是存在的,要完全消除脉动,则必须使式(1-39)中的交变分量等于零,即Fgp1+F:p2+2Fdp1Fdp2cos2矽=0要满足上述条件,应使(1)Fdp1=Fdp2;
即而√2仍″Rmδ1 ’R缶δ2+X备2,所以s1S2Φ2m=u代入式(1-38)即(N)Fdmax=Fdp1+Fdp2最小值为Fdmin=Fap1+Fdp2Φ?
作用在衔铁上总的吸力为Fd=Fd1+Fd2=Fdp1+Fdp2ˉFdp1cos2‘妙莎―Fdp2cos(2‘v矽一2砂) (N)(1-38)
式(1-38)中后两项是同频率的交变分量,其矢量图如图1-27所示。
图中0⒕表示Fd1的交变分量,OB表示Fd2的交变分量,oC是两者的合成矢量。则二交变分量合成后为Fdmcos2弼+Fdp2c°s(2耐~2¢)
Fipl+F:p2+2Fdp1Fdp2cos2矽
×cos(2弼一矽)
吸力交变分量矢量图
Fd=Fdp1+Fdp2
F:p1+F:p2+2Fdp1Fdp2cos2砂cos(2m莎―矽)(1-39)
由式.(1-38)可见,合成吸力最大值为
F:p1+F:p2+2Fdp1Fdp2cos2矽 (N)
F:pl+F:p2+2Fdp1Fdp2cos2矽 (N)
最小值大于反力,即Fdmin)>FF
Φδ1(ωf)、Φδ2(‘记9莎),Fd1(α,莎),Fd2(弼)和F2(耐)的关系曲线如图1-28示。
必须指出,即使满足式(1-40),吸力的脉动还是存在的,要完全消除脉动,则必须使式(1-39)中的交变分量等于零,即Fgp1+F:p2+2Fdp1Fdp2cos2矽=0,要满足上述条件.



 公网安备44030402000607
公网安备44030402000607





