正弦波公式的推导
发布时间:2013/10/26 21:17:47 访问次数:5368
当沿着正弦波水平轴移动时,角度增加,OP215FZ并且幅度(沿着y轴的高度)是变化的。在任何给定昀时刻,正弦波的幅度可以用相位角和振幅(最大值)来描述,因此也就可以表示为相位复矢量( phasor)。相位复矢量是一个既具有幅度又具有方向的量。相位复矢量的图解表示为绕着一个固定点旋转的箭头。正弦波相位复矢量的长度是峰值(振幅),而它旋转时的角度位置是相位角。一个完整的正弦波可以看成是相位复矢量旋转360。。
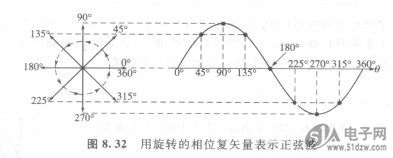
图8.32示出了相位复矢量逆时针方向完成全部的360。旋转。如果相位复矢量的末端映射到一个相位角沿着水平轴移动的图中,正弦波就被“描绘”出来。在相位复矢量的每一个角度位置,有一个对应的振幅值。正如所看见的,在90。和270。,正弦波的幅度最大,并且对应于相位复矢量的长度。在O。和180。,因为相位复矢量在这两点处于水平位置,因此正弦波等于O。
图8. 32用旋转的相位复矢量表示正弦波
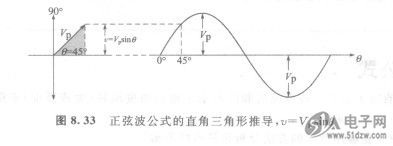
检查一下在一个特定的角度,相位复矢量的表示。图8.33示出了在45。角度的位置电压相位复矢量以及在正弦波上的对应点。在这一点正弦波的瞬时值t,与相位复矢量的位置(角度)和长度(振幅)都有关。从相位复矢量的顶点向下到水平轴的垂直距离代表了正弦波在那一点的瞬时值。注意,当从相位复矢量的顶点向下画出到水平轴的垂直线时,就形成了直角三角形( right triangle),如图8.33所示。相位复矢量的长度是直角三角形的斜边(hypotenuse),而垂直投影是正对着的边。根据三角学,直角三角形的对边等于三角形的斜边乘以角度e的正弦。在这里,相位复矢量的长度是正弦波电压的峰值VP.
当沿着正弦波水平轴移动时,角度增加,OP215FZ并且幅度(沿着y轴的高度)是变化的。在任何给定昀时刻,正弦波的幅度可以用相位角和振幅(最大值)来描述,因此也就可以表示为相位复矢量( phasor)。相位复矢量是一个既具有幅度又具有方向的量。相位复矢量的图解表示为绕着一个固定点旋转的箭头。正弦波相位复矢量的长度是峰值(振幅),而它旋转时的角度位置是相位角。一个完整的正弦波可以看成是相位复矢量旋转360。。

图8.32示出了相位复矢量逆时针方向完成全部的360。旋转。如果相位复矢量的末端映射到一个相位角沿着水平轴移动的图中,正弦波就被“描绘”出来。在相位复矢量的每一个角度位置,有一个对应的振幅值。正如所看见的,在90。和270。,正弦波的幅度最大,并且对应于相位复矢量的长度。在O。和180。,因为相位复矢量在这两点处于水平位置,因此正弦波等于O。
图8. 32用旋转的相位复矢量表示正弦波

检查一下在一个特定的角度,相位复矢量的表示。图8.33示出了在45。角度的位置电压相位复矢量以及在正弦波上的对应点。在这一点正弦波的瞬时值t,与相位复矢量的位置(角度)和长度(振幅)都有关。从相位复矢量的顶点向下到水平轴的垂直距离代表了正弦波在那一点的瞬时值。注意,当从相位复矢量的顶点向下画出到水平轴的垂直线时,就形成了直角三角形( right triangle),如图8.33所示。相位复矢量的长度是直角三角形的斜边(hypotenuse),而垂直投影是正对着的边。根据三角学,直角三角形的对边等于三角形的斜边乘以角度e的正弦。在这里,相位复矢量的长度是正弦波电压的峰值VP.
 热门点击
热门点击
- 常小数点的七段共阴极半导体数码管BS201的
- 由3AD18型功率管组成的乙类推挽功率放大器
- 正弦波公式
- 常见的BCD编码
- 量化和编码
- 正弦波公式的推导
- 阻抗和相角随频率的变化
- 七段字形译码器
- 可变电容器及其主要参数
- 吸锡电烙铁的外形与结构
 推荐技术资料
推荐技术资料
- 自制经典的1875功放
- 平时我也经常逛一些音响DIY论坛,发现有很多人喜欢LM... [详细]

 公网安备44030402000607
公网安备44030402000607





