模型的调整
发布时间:2013/2/25 20:05:28 访问次数:840
模拟所需的最重要的参数是ICD3弹波材料的杨氏模量和整个系统的损耗因数。
弹波材料的杨氏模量是通过反演法获得的。制作一个如图5所示的实验用驱动器,双弹波但没有振膜。因为这个系统的质量是很容易得到的,下面只要调整数值模型的参数,使得数值模型的共振频率与实验用驱动器测出来的阻抗曲线(图6)的共振频率吻合。
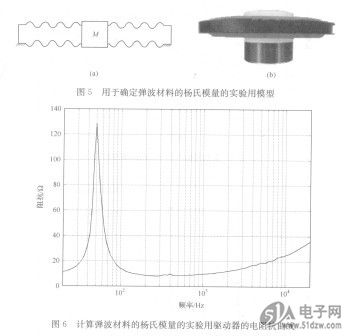
图6计算弹波材料的杨氏模量的实验用驱动器的电阻抗曲线
整个系统的损耗因数是通过调整振膜位移,使其为单自由度( SDOF)系统。而这里所用的数值模型和实验用模型都是完整的振动系统,包括振膜。
图7是在输入电压为10V、15V和20V的情况下,用Klippel Analyzer sys-tem[10]测量得到实验用扬声器单元的振膜位移。
通过调节阻尼矩阵[C]中的系数口和卢,可以得到合适的损耗因数,使其完全符合SDOF系统。这样,数值模拟结果和实验结果就可以完全吻合。
模拟所需的最重要的参数是ICD3弹波材料的杨氏模量和整个系统的损耗因数。
弹波材料的杨氏模量是通过反演法获得的。制作一个如图5所示的实验用驱动器,双弹波但没有振膜。因为这个系统的质量是很容易得到的,下面只要调整数值模型的参数,使得数值模型的共振频率与实验用驱动器测出来的阻抗曲线(图6)的共振频率吻合。

图6计算弹波材料的杨氏模量的实验用驱动器的电阻抗曲线
整个系统的损耗因数是通过调整振膜位移,使其为单自由度( SDOF)系统。而这里所用的数值模型和实验用模型都是完整的振动系统,包括振膜。
图7是在输入电压为10V、15V和20V的情况下,用Klippel Analyzer sys-tem[10]测量得到实验用扬声器单元的振膜位移。
通过调节阻尼矩阵[C]中的系数口和卢,可以得到合适的损耗因数,使其完全符合SDOF系统。这样,数值模拟结果和实验结果就可以完全吻合。



 公网安备44030402000607
公网安备44030402000607





