卡诺图化简
发布时间:2012/2/14 20:18:40 访问次数:5232
卡诺圈所圈方格的个数为2”,即2个、4个、8个……所圈图形构成方形(或矩形)。2”个最小项合并成一项时可以消去犯个变量。如2z =4个小方格合并时可消去2个变量;23 =8个小方格合并成一项时可消去3个变量;若将卡诺图中所有的小方格都用卡诺圈圈起来,化简结果为1。 PC8270MTPUQLDA
(2)用卡诺图化简逻辑函数的步骤
①画(逻辑函数的)卡诺图。
②画卡诺圈,即用卡诺圈包围2”个为1的方格群,合并最小项,写出乘积项。
③写表达式。先按照留同去异原则写出每个卡诺圈的乘积项,再将所有卡诺圈的乘积项加起来,即为化简后的与或表达式。
利用卡诺图进行逻辑函数化简时,应遵循以下原则:
①卡诺圈越大越好。合并最小项时,包围的最小项越多,消去的变量就越多,化简结果就越简单。
②卡诺圈的个数越少越好,这样化简后的乘积项就少。
③不能漏项。必须把组成函数的全部最小项都圈完。
用卡诺图化简函数
①先将函数y填入四变量卡诺图中,如图7 -12所示。
②画卡诺圈,从图7 -12中看出,包含的卡诺圈虽然最大,但它不是独立的,这4个最小项已被其他4个卡诺圈圈过了。
③提取每个卡诺圈的公因子构成乘积项,然后将这些乘积项相加,
用卡诺图化简函数
①先将函数y填人四变量卡诺图,如图7 -13所示。
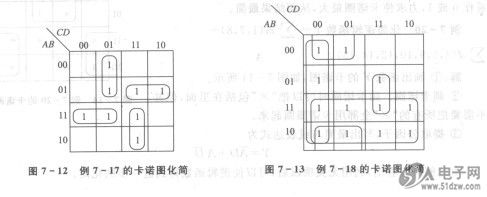
②画卡诺圈。
③提取每个卡诺圈的公因子作乘积项,将这些乘积项相加,就可得到化简后的逻辑函数。
卡诺圈所圈方格的个数为2”,即2个、4个、8个……所圈图形构成方形(或矩形)。2”个最小项合并成一项时可以消去犯个变量。如2z =4个小方格合并时可消去2个变量;23 =8个小方格合并成一项时可消去3个变量;若将卡诺图中所有的小方格都用卡诺圈圈起来,化简结果为1。 PC8270MTPUQLDA
(2)用卡诺图化简逻辑函数的步骤
①画(逻辑函数的)卡诺图。
②画卡诺圈,即用卡诺圈包围2”个为1的方格群,合并最小项,写出乘积项。
③写表达式。先按照留同去异原则写出每个卡诺圈的乘积项,再将所有卡诺圈的乘积项加起来,即为化简后的与或表达式。
利用卡诺图进行逻辑函数化简时,应遵循以下原则:
①卡诺圈越大越好。合并最小项时,包围的最小项越多,消去的变量就越多,化简结果就越简单。
②卡诺圈的个数越少越好,这样化简后的乘积项就少。
③不能漏项。必须把组成函数的全部最小项都圈完。
用卡诺图化简函数
①先将函数y填入四变量卡诺图中,如图7 -12所示。
②画卡诺圈,从图7 -12中看出,包含的卡诺圈虽然最大,但它不是独立的,这4个最小项已被其他4个卡诺圈圈过了。
③提取每个卡诺圈的公因子构成乘积项,然后将这些乘积项相加,
用卡诺图化简函数
①先将函数y填人四变量卡诺图,如图7 -13所示。

②画卡诺圈。
③提取每个卡诺圈的公因子作乘积项,将这些乘积项相加,就可得到化简后的逻辑函数。
上一篇:用卡诺图化简逻辑函数
上一篇:具有无关项的逻辑函数的化简



 公网安备44030402000607
公网安备44030402000607





