UTC8550SECB导体电阻的能量
发布时间:2019/10/28 21:36:19 访问次数:842
UTC8550SECB向外散发通过求解热平衡方程,可求出接触区与导体区交界处的温升为
t=i2p/kmq+uci/kmq (2-11)
式中u―导体的电阻系数(Ω・m)和导热系数(W/cm・K);
Κ―导体的散热系数(W/cm2・K);
m,q―导体的周长(m)和截面(m2);
i,uc―触点电流(A)和触点压降(V)。
式(2-11)中的第一项
t1=i2/kmq
可以看成是导体电阻的能量损耗所引起的温升;第二项
t2=uci/kmq (2-12)
可以看成是接触电阻上能量损耗在导体中的传输和散发,在接触区与导体区的交界处造成的温升。
实际上触点最高温升要高于由式(2-11)所表示的交界处的温升。这是因为接触面上以及收缩区内的热量要向外传送,接触区内又造成一个热的“压降”。因此触点的最高温升是
tm=tc+t1+t2 (2-14)
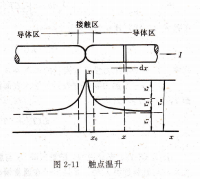
通过对接触区内电流场和温度场的分析,可以找出一个rc的近似表达式为
tc=uc2/8p (2-15)
对于不同的触点,式(2-14)中三项温升之间的比例也不相同。如在大电流的断路器和接触器中,触点压力很大,使⒒很小,rc一项所占比例不大。而这种电器产品导体截面是按发热条件决定的,电流密度一般较大,因此rl这一项占的比例较大。对于小电流的继电器触点则相反,其导体截面是按一些机械性能的要求决定的,电流密度很低,r1很小。而这种产品往往出于对灵敏度的要求,触点的压力很低,c较大,使△在总温升中占了主要地位。
式(2-14)虽然是从一个特殊例子中推导出来的,但它所代表的概念适用于各种触点。
接触压降,触点的最高温升在接触面的深处,无法直接测量,而公式(2-15)提供的关系可知,通过测量接触压降uc便可达到间接测量tc的目的。
逻辑函数产生器,根据8选1数据选择器输出与输人的关系式(4.4.7)有式中mi是地址选择输入端s2、s1、sO构成的最小项。数据输入作为控制信号,当DJ=1时,其对应的最小项祝氵在表达式中出现,当Di=0时,对应的最小项就不出现。利用这一点将函数变换成最小项表达式,函数的变量接入地址选择输入端,就可以实现组合逻辑函数。
例4,4,7 试用8选1数据选择器74HC151产生逻辑函数L=ABC+ABC+ABc
解:把所给的函数式变换成最小项表达式L=ABC+ABC+ABC+ABC
将上式写成如下形式
L=m3D3+5D5+m6D6+m7D7
显然D3、D5、D6、D7都应该等于1,而式中没有出现的最小项mO、m1、m2、m4对应的数据输入端D。、D1、D2、D4都应该等于0,并将使能端接低电平。由此可画出该逻辑函数产生器的逻辑图,如图4.4,24所示。
通过上面例题可以看出,与使用各种逻辑门设计组合逻辑电需对函数化简。路相比,数据选择器的好处是无的转成的并/串行转换的电路图。选择照图中所给波形从数据并行输入转换成串行输出(a)电路图 (b)时序图若干典型的绍合逻辑集成电路.
UTC8550SECB向外散发通过求解热平衡方程,可求出接触区与导体区交界处的温升为
t=i2p/kmq+uci/kmq (2-11)
式中u―导体的电阻系数(Ω・m)和导热系数(W/cm・K);
Κ―导体的散热系数(W/cm2・K);
m,q―导体的周长(m)和截面(m2);
i,uc―触点电流(A)和触点压降(V)。
式(2-11)中的第一项
t1=i2/kmq
可以看成是导体电阻的能量损耗所引起的温升;第二项
t2=uci/kmq (2-12)
可以看成是接触电阻上能量损耗在导体中的传输和散发,在接触区与导体区的交界处造成的温升。
实际上触点最高温升要高于由式(2-11)所表示的交界处的温升。这是因为接触面上以及收缩区内的热量要向外传送,接触区内又造成一个热的“压降”。因此触点的最高温升是
tm=tc+t1+t2 (2-14)

通过对接触区内电流场和温度场的分析,可以找出一个rc的近似表达式为
tc=uc2/8p (2-15)
对于不同的触点,式(2-14)中三项温升之间的比例也不相同。如在大电流的断路器和接触器中,触点压力很大,使⒒很小,rc一项所占比例不大。而这种电器产品导体截面是按发热条件决定的,电流密度一般较大,因此rl这一项占的比例较大。对于小电流的继电器触点则相反,其导体截面是按一些机械性能的要求决定的,电流密度很低,r1很小。而这种产品往往出于对灵敏度的要求,触点的压力很低,c较大,使△在总温升中占了主要地位。
式(2-14)虽然是从一个特殊例子中推导出来的,但它所代表的概念适用于各种触点。
接触压降,触点的最高温升在接触面的深处,无法直接测量,而公式(2-15)提供的关系可知,通过测量接触压降uc便可达到间接测量tc的目的。
逻辑函数产生器,根据8选1数据选择器输出与输人的关系式(4.4.7)有式中mi是地址选择输入端s2、s1、sO构成的最小项。数据输入作为控制信号,当DJ=1时,其对应的最小项祝氵在表达式中出现,当Di=0时,对应的最小项就不出现。利用这一点将函数变换成最小项表达式,函数的变量接入地址选择输入端,就可以实现组合逻辑函数。
例4,4,7 试用8选1数据选择器74HC151产生逻辑函数L=ABC+ABC+ABc
解:把所给的函数式变换成最小项表达式L=ABC+ABC+ABC+ABC
将上式写成如下形式
L=m3D3+5D5+m6D6+m7D7
显然D3、D5、D6、D7都应该等于1,而式中没有出现的最小项mO、m1、m2、m4对应的数据输入端D。、D1、D2、D4都应该等于0,并将使能端接低电平。由此可画出该逻辑函数产生器的逻辑图,如图4.4,24所示。
通过上面例题可以看出,与使用各种逻辑门设计组合逻辑电需对函数化简。路相比,数据选择器的好处是无的转成的并/串行转换的电路图。选择照图中所给波形从数据并行输入转换成串行输出(a)电路图 (b)时序图若干典型的绍合逻辑集成电路.
上一篇:SI9922触点接触压降极易测量



 公网安备44030402000607
公网安备44030402000607





