热敏电阻特性及分段线性化
发布时间:2014/7/30 20:24:12 访问次数:1138
这就是用来标度变换的插值多项式,将采样测得的电阻值R代入上式,即可获得被测温度f。
显然,插值点的选择对于逼近的精度有很大的影响。通常在函数y= f(x)的曲线上曲率大的地方应适当加密插值点。
一般来说,G5209S31U增加插值点和多项式的次数能提高逼近精度。但同时会增加计算时间,而且在某些情况下反而可能会造成误差的摆动;另一方面,对于那些带拐点的函数,如果用一个多项式去逼近,将会产生较大的误差。
为了提高逼近精度,且不占用过多的机时,较好的方法是采用分段插值法。分段插值法是将被逼近的函数根据其变化情况分成几段.然后将每一段区间分别用直线或抛物线去逼近。分段插值的分段点的选取可按实际曲线的情况灵活决定,既可以采用等距分段法,又可采用非等距分段法。
如上例热敏电阻温度£与电阻值R的插值多项式,其计算量较大,程序也较复杂。为使计算简单,提高实时性,可采用分段线性插值公式或称分段线性化的方法,即用多段折线代替曲线进行计算。
根据表7 -1中的数据制成图7-4所示的热敏电阻特性并分段线性化,其中曲线为热敏电阻的负温度一电阻特性,折线£。./i、L2代替或逼近曲线。当获取某个采样值R后,先判断R的大小处于哪一折线段内,然后就可按相应段的线性化公式计算出标度变换值。
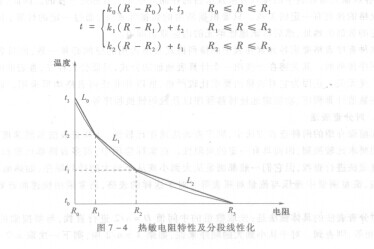

这就是用来标度变换的插值多项式,将采样测得的电阻值R代入上式,即可获得被测温度f。
显然,插值点的选择对于逼近的精度有很大的影响。通常在函数y= f(x)的曲线上曲率大的地方应适当加密插值点。
一般来说,G5209S31U增加插值点和多项式的次数能提高逼近精度。但同时会增加计算时间,而且在某些情况下反而可能会造成误差的摆动;另一方面,对于那些带拐点的函数,如果用一个多项式去逼近,将会产生较大的误差。
为了提高逼近精度,且不占用过多的机时,较好的方法是采用分段插值法。分段插值法是将被逼近的函数根据其变化情况分成几段.然后将每一段区间分别用直线或抛物线去逼近。分段插值的分段点的选取可按实际曲线的情况灵活决定,既可以采用等距分段法,又可采用非等距分段法。
如上例热敏电阻温度£与电阻值R的插值多项式,其计算量较大,程序也较复杂。为使计算简单,提高实时性,可采用分段线性插值公式或称分段线性化的方法,即用多段折线代替曲线进行计算。
根据表7 -1中的数据制成图7-4所示的热敏电阻特性并分段线性化,其中曲线为热敏电阻的负温度一电阻特性,折线£。./i、L2代替或逼近曲线。当获取某个采样值R后,先判断R的大小处于哪一折线段内,然后就可按相应段的线性化公式计算出标度变换值。


 热门点击
热门点击
- 用74LS160实现十四进制计数器
- 模拟量输入通道的结构组成
- LabVIEW的视觉助手
- DI/DO模板
- 自动/手动双向无扰动切换
- 测量TTL信号频率和周期
- 无级调速电风扇控制电路详解
- 数字信号通道设置
- LED动态显示软件译码程序流程
- 自动整理程序框图
 推荐技术资料
推荐技术资料
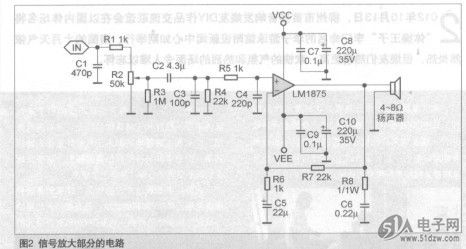
- 自制经典的1875功放
- 平时我也经常逛一些音响DIY论坛,发现有很多人喜欢LM... [详细]

 公网安备44030402000607
公网安备44030402000607





