方波波形与瞬变
发布时间:2013/7/7 17:34:18 访问次数:1095
前面我们大致提到,方波XF2M-6015-1AH含有瞬变成分。可以将方波看作是,一个直流信号每经一定的时间间隔,就突然出现极性的反转。在极性反转的瞬间,信号电压突然地由负变正,或突然地由正变负。在方波边沿处的突然变化是瞬变的,也由于发生得如此之快,因而必定含有较大比例的高频成分。尽管我们己知道方波含有高频成分,但还应知道,这些高频成分仅是在方波边沿处聚集,频率响应如果有何变化,将会在边沿处显现出来。
我们已从频率的角度研究方波。现在,要从时间的角度研究他的瞬变,以及在CR网络和LR网络中的表现。
适当用一些图形配上相应说明,最容易让人明白这方面的内容。确实有公式可供使用,但我们很少需要用到它们。
在电子学中,阶跃( step)是指电压或电流在数量上的瞬时(instantaneous)变化。这是很有用的理论概念,用于研究电路的瞬时响应。先看一看阶跃电压经过电阻加到电容两端的情况,如图1.31所示。
开始时,电容已放完电(%=O)。阶跃电压从V切换至+V,这个瞬变大部分是由高频信号构成。电容的电抗与频率成反比,因此,对这些高频信号而言,电容呈短路特性。因为是短路,此时的电容两端没有电压出现。电阻两端因而承担了所加的全部电压,电阻上流经的电流由欧姆定律决定。这个电流还流经电容.开始对电容进行充电。充电时,电容电压逐渐上升,直至充电完毕后才停止,流经的电流也就变为零。由于充电完毕后电容电流为零(/c=0),于是有/R=O,因此VR=O。我们可以画出电容电压和电阻电压的两个变化曲线图,如图1.32所示。
图1.32 CR电路在电压阶跃变化下的指数响应
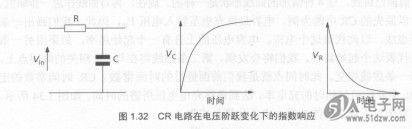
须注意两点。一是两个变化图的曲线都是指数( exponential)曲线(稍后对“指数”一词作进一步说明)。二是CR电路(以及LR电路)加上阶跃电压后,电压曲线或电流曲线必定为这两条曲线中的一条。知道这一规律后,我们画图时只需选出正确的参照曲线即可。
前面我们大致提到,方波XF2M-6015-1AH含有瞬变成分。可以将方波看作是,一个直流信号每经一定的时间间隔,就突然出现极性的反转。在极性反转的瞬间,信号电压突然地由负变正,或突然地由正变负。在方波边沿处的突然变化是瞬变的,也由于发生得如此之快,因而必定含有较大比例的高频成分。尽管我们己知道方波含有高频成分,但还应知道,这些高频成分仅是在方波边沿处聚集,频率响应如果有何变化,将会在边沿处显现出来。
我们已从频率的角度研究方波。现在,要从时间的角度研究他的瞬变,以及在CR网络和LR网络中的表现。
适当用一些图形配上相应说明,最容易让人明白这方面的内容。确实有公式可供使用,但我们很少需要用到它们。
在电子学中,阶跃( step)是指电压或电流在数量上的瞬时(instantaneous)变化。这是很有用的理论概念,用于研究电路的瞬时响应。先看一看阶跃电压经过电阻加到电容两端的情况,如图1.31所示。
开始时,电容已放完电(%=O)。阶跃电压从V切换至+V,这个瞬变大部分是由高频信号构成。电容的电抗与频率成反比,因此,对这些高频信号而言,电容呈短路特性。因为是短路,此时的电容两端没有电压出现。电阻两端因而承担了所加的全部电压,电阻上流经的电流由欧姆定律决定。这个电流还流经电容.开始对电容进行充电。充电时,电容电压逐渐上升,直至充电完毕后才停止,流经的电流也就变为零。由于充电完毕后电容电流为零(/c=0),于是有/R=O,因此VR=O。我们可以画出电容电压和电阻电压的两个变化曲线图,如图1.32所示。
图1.32 CR电路在电压阶跃变化下的指数响应

须注意两点。一是两个变化图的曲线都是指数( exponential)曲线(稍后对“指数”一词作进一步说明)。二是CR电路(以及LR电路)加上阶跃电压后,电压曲线或电流曲线必定为这两条曲线中的一条。知道这一规律后,我们画图时只需选出正确的参照曲线即可。
上一篇:域下的方波波形及频域下的方波频谱
上一篇:指数曲线与时间常数T的对应关系



 公网安备44030402000607
公网安备44030402000607





