用双极晶体管电路能够表现任意函数
发布时间:2013/6/13 14:52:57 访问次数:647
使用双极晶体管,能够构G6D-1A-ASI-12V成计算r2+2r+l之类的任意多项式,或者(r-l)/(z2+z+1)等有理式的电路。
使用泰勒(Taylor)展开或者马克劳林(Maclaurin)展开,就能够依据多项式对任意的函数进行近似。应用跨导线性原理,就能够构成具有任意的输入输出关系的电路。只是这么说,也许还是理解不深刻,还需要通过例子来体验到它的强大功能。
跨导线性原理的推导
现在以图12.1的电路为例,来导出跨导线性原理。跨导线性原理是关于经由双极晶体管的基极与集电极所形成的回路的关系的法则。图12.1的电路中,形成了通过基极与集电极的甸路(叫做跨导线性回路)。对于这个回路,应用基尔霍夫电压定律,可以写出如下关系式
BEl +V BE2BE3BE4 +V BE5BE6 (12.2)
VBEl+VBE2+VBE3~VBE4+VBE5+VBE6
这里,从Q,到Q。的基极一集电极中间的箭头指向逆时针(CCW),Q4到Q6的基极一集电极之间是顺时针(CW)。由此,式(12.8)的左边描述的是CCW的电流,右边描述的是CW的电流。
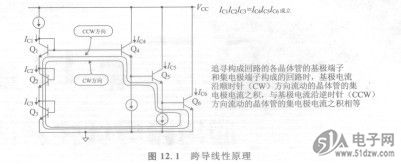
把式(12.8)扩展到一般形式,那就是对于含有任意数目的晶体管的跨导线性回路,式(12.1)成立。
使用双极晶体管,能够构G6D-1A-ASI-12V成计算r2+2r+l之类的任意多项式,或者(r-l)/(z2+z+1)等有理式的电路。
使用泰勒(Taylor)展开或者马克劳林(Maclaurin)展开,就能够依据多项式对任意的函数进行近似。应用跨导线性原理,就能够构成具有任意的输入输出关系的电路。只是这么说,也许还是理解不深刻,还需要通过例子来体验到它的强大功能。
跨导线性原理的推导
现在以图12.1的电路为例,来导出跨导线性原理。跨导线性原理是关于经由双极晶体管的基极与集电极所形成的回路的关系的法则。图12.1的电路中,形成了通过基极与集电极的甸路(叫做跨导线性回路)。对于这个回路,应用基尔霍夫电压定律,可以写出如下关系式
BEl +V BE2BE3BE4 +V BE5BE6 (12.2)
VBEl+VBE2+VBE3~VBE4+VBE5+VBE6
这里,从Q,到Q。的基极一集电极中间的箭头指向逆时针(CCW),Q4到Q6的基极一集电极之间是顺时针(CW)。由此,式(12.8)的左边描述的是CCW的电流,右边描述的是CW的电流。

把式(12.8)扩展到一般形式,那就是对于含有任意数目的晶体管的跨导线性回路,式(12.1)成立。
上一篇:应用跨导线性原理
上一篇:温度变化时,跨导线性电路是稳定的


 公网安备44030402000607
公网安备44030402000607





