CY7C4205-35AC如何实现带阻滤波电路的功能
发布时间:2019/11/11 17:58:25 访问次数:798
CY7C4205-35AC二阶有源带阻滤波电路,前已指出,与带通滤波电路相反,带阻滤波电路是用来抑制或衰减某一频段的信号,而让该频段以外的所有信号通过。这种滤波电路也叫陷波电路,经常用于电子系统抗干扰。
如何实现带阻滤波电路的功能呢?显然,如果从输入信号中减去带通滤波电路处理过的信号,就可得到带阻信号。这是实现带阻滤波的思路之一,读者可自行分析。这里要讨论的是另一种方案,即双T带阻滤波电路。
电路如图9.3.15所示,由节点导纳方程不难导出电路的传递函数为
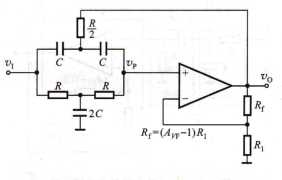
a(s)=vo(s)/vi(s)=avf[1+(s/wo)2]
式中wo=1/rc,既是特性角频率,也是带阻滤波电路的中心角频率,AvF=Ao=1+rf/r1为带阻滤波电路的通带电压增益;q=1/2(2-ao)。如果A0=1,则o=0,5,增加AO,o将随之升高。当A0趋近2时,o趋向无穷大。因此,A。愈接近2, |A|愈大,可使带阻滤波电路的选频特性愈好,即阻断的频率范围愈窄。图9,3.15所示带阻滤波电路的幅频特性如图9,3,16所示。
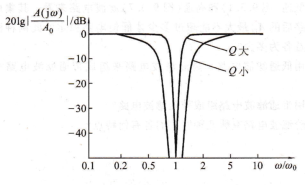
图9.3.16 图9.3.15所示带阻滤波电路的幅频特性
本节附录:巴特沃思传递函数
前已指出,对于低通滤波电路来说,3 dB截止角频率ωc=ωHc因此由式(9,2,3)和式(9.3.7)可得刀阶低通滤波电路幅频响应的一般形式
|A(Jω/wc)|=ao/1+k2((w/wc)2+k4(w/wc)4 (⒐⒊20)
因为|A(jω/ωc)|2是偶次函数,所以ω/ωc的奇次幂不会出现。考虑到在ω/ωc(1)时,巴特沃思低通滤波电路的幅频响应是平坦的c而在ω/ωc(1时,主要是ω/ωc的低次项对分母起作用而使|A(jω/ωc)|下降。如果|A(jω/ωc)|只与ω/ωc的高次项有关,则能较好地满足上述条件。因此式(9.3.20)可写成
|A(Jω)/wc)|=ao/1+(w?wc)2n (⒐3.21)
1+K2n(ω/ωc)
这就是巴特沃思低通滤波电路的特性方程。
由于ω/ωc=1时,增益减小3 dB,由式(9.3.21)有A02/2=A02/(1+Κ2n),可得k2n=1,因而式(⒐3.21)变为
|A(Jω/wc)|2=ao2/1+k2n(w+wc)2n (⒐3.22)
式(9.3.23)一般可简写为 |A(jω)|=0
从有源低通(图9.3,1)和高通(图9.3.7)滤波电路来看,其集成运放接成同相放大电路后的avf最大不能超过多少才能使电路稳定9此两种滤波电路的通带电压增益各为多少?
能否利用低通滤波电路、高通滤波电路来组成带通滤波电路?组成的条件是什么?
能否利用带通滤波电路组成带阻滤波电路?
常用高阶滤波电路有哪几种?它们各有何特点?
前面讨论的有源RC滤波电路,由于要求有较大的电容和精确的RC时间常数,以至在芯片上制造集成组件难度较大,甚至不可能。随着MOS工艺迅速发展,由MOS开关电容和运放组成的开关电容滤波器①已于1975年实现了单片集成化。这种滤波器不需要模数转换器,可以对模拟量的离散值直接进行处理。与数字滤波器比较,省略了量化过程,因而具有处理速度快、整体结构简单等优点。此外,它制造简易,价廉,因而受到各方面的重视,经过30多年的发展,开关电容滤波器的性能已达到相当高的水平,大有取代一般有源滤波器的趋势。
基本原理,开关电容滤波器的基本原理是由电路两节点间接有带高速开关的电容器,
其效果相当于该两节点问连接一个电阻。图9,4.1a所示是一个有源RC积分器。在图9.4.1b中,用一个接地电容器C1和用作开关的源漏两极可互换的增强型MOSFET T1、T2(此处用的是简化符号)来代替输人电阻r1。
图中T1、T2用一个不重叠的两相时钟脉冲来驱动。图9.4.1c画出了这种时钟波形φl和φ2。假定时钟频率五(=1/rc)远高于信号频率。那么,在φ1为高电平时,TI导通而T2截止(见图d)。此时Cl与输人信号pi相连并被充电,即有开关电容滤波器的英文名称为Switched Capacitor Fmcr,简称SCF。
CY7C4205-35AC二阶有源带阻滤波电路,前已指出,与带通滤波电路相反,带阻滤波电路是用来抑制或衰减某一频段的信号,而让该频段以外的所有信号通过。这种滤波电路也叫陷波电路,经常用于电子系统抗干扰。
如何实现带阻滤波电路的功能呢?显然,如果从输入信号中减去带通滤波电路处理过的信号,就可得到带阻信号。这是实现带阻滤波的思路之一,读者可自行分析。这里要讨论的是另一种方案,即双T带阻滤波电路。
电路如图9.3.15所示,由节点导纳方程不难导出电路的传递函数为

a(s)=vo(s)/vi(s)=avf[1+(s/wo)2]
式中wo=1/rc,既是特性角频率,也是带阻滤波电路的中心角频率,AvF=Ao=1+rf/r1为带阻滤波电路的通带电压增益;q=1/2(2-ao)。如果A0=1,则o=0,5,增加AO,o将随之升高。当A0趋近2时,o趋向无穷大。因此,A。愈接近2, |A|愈大,可使带阻滤波电路的选频特性愈好,即阻断的频率范围愈窄。图9,3.15所示带阻滤波电路的幅频特性如图9,3,16所示。

图9.3.16 图9.3.15所示带阻滤波电路的幅频特性
本节附录:巴特沃思传递函数
前已指出,对于低通滤波电路来说,3 dB截止角频率ωc=ωHc因此由式(9,2,3)和式(9.3.7)可得刀阶低通滤波电路幅频响应的一般形式
|A(Jω/wc)|=ao/1+k2((w/wc)2+k4(w/wc)4 (⒐⒊20)
因为|A(jω/ωc)|2是偶次函数,所以ω/ωc的奇次幂不会出现。考虑到在ω/ωc(1)时,巴特沃思低通滤波电路的幅频响应是平坦的c而在ω/ωc(1时,主要是ω/ωc的低次项对分母起作用而使|A(jω/ωc)|下降。如果|A(jω/ωc)|只与ω/ωc的高次项有关,则能较好地满足上述条件。因此式(9.3.20)可写成
|A(Jω)/wc)|=ao/1+(w?wc)2n (⒐3.21)
1+K2n(ω/ωc)
这就是巴特沃思低通滤波电路的特性方程。
由于ω/ωc=1时,增益减小3 dB,由式(9.3.21)有A02/2=A02/(1+Κ2n),可得k2n=1,因而式(⒐3.21)变为
|A(Jω/wc)|2=ao2/1+k2n(w+wc)2n (⒐3.22)
式(9.3.23)一般可简写为 |A(jω)|=0
从有源低通(图9.3,1)和高通(图9.3.7)滤波电路来看,其集成运放接成同相放大电路后的avf最大不能超过多少才能使电路稳定9此两种滤波电路的通带电压增益各为多少?
能否利用低通滤波电路、高通滤波电路来组成带通滤波电路?组成的条件是什么?
能否利用带通滤波电路组成带阻滤波电路?
常用高阶滤波电路有哪几种?它们各有何特点?
前面讨论的有源RC滤波电路,由于要求有较大的电容和精确的RC时间常数,以至在芯片上制造集成组件难度较大,甚至不可能。随着MOS工艺迅速发展,由MOS开关电容和运放组成的开关电容滤波器①已于1975年实现了单片集成化。这种滤波器不需要模数转换器,可以对模拟量的离散值直接进行处理。与数字滤波器比较,省略了量化过程,因而具有处理速度快、整体结构简单等优点。此外,它制造简易,价廉,因而受到各方面的重视,经过30多年的发展,开关电容滤波器的性能已达到相当高的水平,大有取代一般有源滤波器的趋势。
基本原理,开关电容滤波器的基本原理是由电路两节点间接有带高速开关的电容器,
其效果相当于该两节点问连接一个电阻。图9,4.1a所示是一个有源RC积分器。在图9.4.1b中,用一个接地电容器C1和用作开关的源漏两极可互换的增强型MOSFET T1、T2(此处用的是简化符号)来代替输人电阻r1。
图中T1、T2用一个不重叠的两相时钟脉冲来驱动。图9.4.1c画出了这种时钟波形φl和φ2。假定时钟频率五(=1/rc)远高于信号频率。那么,在φ1为高电平时,TI导通而T2截止(见图d)。此时Cl与输人信号pi相连并被充电,即有开关电容滤波器的英文名称为Switched Capacitor Fmcr,简称SCF。
上一篇:HPMX3001开关电容滤波器




 公网安备44030402000607
公网安备44030402000607





