0362007.M 逻辑函数简逻辑函数的方法
发布时间:2019/10/9 21:38:25 访问次数:2258
0362007.M例2.2.5 一个逻辑电路有4个输入逻辑尽可能大 ,结果包可以获得逻辑函数简逻辑函数的方法最简与一或D变量A、 B、 C、 D,它的真值表如表2.2.3所示 ,用卡诺图法求化简的与一或表达式及与非图2.2,9例 2.2.4的卡诺图一与非表达式 。
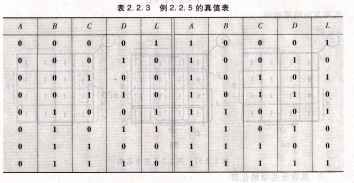
解 :(1)由真值表画出卡诺图,如图2.2.10所示 。
画包围圈合并最小项 ,得简化的与一或表达式。
L=CD+ABD+ABC+ABCD
求与非一与非表达式二次求非
L=CD十ABD+ABC+ABCD
然后利用摩根定律得
L=CD· ABD· ABC· ABCD
利用卡诺图表示逻辑函数式时 ,如果卡诺图中各小方格被1占去了大部分 ,虽然可用包围1的方法进行化简 ,但由于要重复利用1项 ,往往显得零乱而易出错 。这时采用包围0的方法化简更为简单 。即求出非函数L,再对L求非 ,其结果相同,下面举例说明。
化简下列逻辑 函数
L(A,B,C,D)=∑ m(o~3,5~11,13~15)
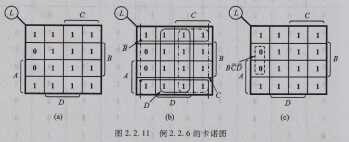
解 :由L画出卡诺图 ,如图2.2.11(a)所示 。
方法一 :用包围1的方法化简 ,如图2.2.11(b)所示 ,得
L=B+C+D
方法二 :用包围0的方法化简 ,如图2.2,11(c)所示 ,得
L=BCD
对L求非
L=B+C+D
两种方法结果相同。
0362007.M例2.2.5 一个逻辑电路有4个输入逻辑尽可能大 ,结果包可以获得逻辑函数简逻辑函数的方法最简与一或D变量A、 B、 C、 D,它的真值表如表2.2.3所示 ,用卡诺图法求化简的与一或表达式及与非图2.2,9例 2.2.4的卡诺图一与非表达式 。

解 :(1)由真值表画出卡诺图,如图2.2.10所示 。
画包围圈合并最小项 ,得简化的与一或表达式。
L=CD+ABD+ABC+ABCD
求与非一与非表达式二次求非
L=CD十ABD+ABC+ABCD
然后利用摩根定律得
L=CD· ABD· ABC· ABCD
利用卡诺图表示逻辑函数式时 ,如果卡诺图中各小方格被1占去了大部分 ,虽然可用包围1的方法进行化简 ,但由于要重复利用1项 ,往往显得零乱而易出错 。这时采用包围0的方法化简更为简单 。即求出非函数L,再对L求非 ,其结果相同,下面举例说明。
化简下列逻辑 函数
L(A,B,C,D)=∑ m(o~3,5~11,13~15)
解 :由L画出卡诺图 ,如图2.2.11(a)所示 。
方法一 :用包围1的方法化简 ,如图2.2.11(b)所示 ,得
L=B+C+D
方法二 :用包围0的方法化简 ,如图2.2,11(c)所示 ,得
L=BCD
对L求非
L=B+C+D
两种方法结果相同。

 热门点击
热门点击
- 双环网接线
- 逐次逼近型A-D转换
- sD92IO型FTU数字量输入输出
- 典型配电线载波通信系统组成
- 数据通信系统的组成,DTE、DCE设备各有哪
- TMs320F206DsP片上外设
- 变电站的功能是接受电能、变换电压和分配电能
- 电力系统的中性点是指星形联结的变压器或发电机
- 环网手拉手馈线故障的处理
- 7150-05-10 电压传输特性
 推荐技术资料
推荐技术资料
- 硬盘式MP3播放器终级改
- 一次偶然的机会我结识了NE0 2511,那是一个远方的... [详细]


 公网安备44030402000607
公网安备44030402000607





