ED1100/4 无关项或任意项
发布时间:2019/10/10 12:07:26 访问次数:2188
ED1100/4具有无关项的化简,实际中经常会遇到这样的问题 ,在真值表内对应于变量的某些取值下 ,函数的值可以是任意的,或者这些变量的取值根本不会出现,这些变量取值所对应的最小项称为无关项或任意项。
无关项的意义在于,它的值可以取0或取1,具体取什么值,可以根据使函数尽量得到简化而定。下面举一个利用无关项化简的例子。
例2.2.7 要求设计一个逻辑电路,能够判断1位十进制数是奇数还是偶数,当十进制数为奇数时,电路输出为1,当十进制数为偶数时,电路输出为0。
解:第一步,列写真值表。用8421BCD码表示十进制数,4位码即为输入变量,当对应的十进制数为奇数时,函数值为1,反之为0,得到表2.2.4所示的真值表。
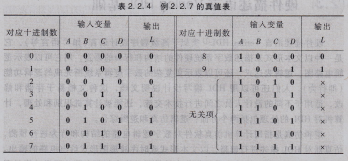
注意,8421BCD码只有10个,表中4位二进制码的后6种组合是无关的,1位十进制数不包括10~15,这些无关状态根本不会出现,这后6种变量组合对应的最小项就是无关项,它们对应的函数值可以任意假设,为0为1都可以,通常以×(或O)表示。
第二步,将真值表的内容填人四变量卡诺图,如图2.2.12所示。

第三步 ,画包围圈 ,此时应利用无关项 ,显然 ,将最小项M13、m15、 M11对应 的方格视为1,可以得到最大的包围圈 ,由此可写出L=D.
若不利用无关项 ,L=AD+BCD,结果复杂得多 。
以上讨论的是从一变量到四变量的卡诺图,并以四变量卡诺图为例,分析了逻辑函数的化简方法。至于更多变量,例如五变量或六变量卡诺图的应用,可参阅文献[3]和[4]。
ED1100/4具有无关项的化简,实际中经常会遇到这样的问题 ,在真值表内对应于变量的某些取值下 ,函数的值可以是任意的,或者这些变量的取值根本不会出现,这些变量取值所对应的最小项称为无关项或任意项。
无关项的意义在于,它的值可以取0或取1,具体取什么值,可以根据使函数尽量得到简化而定。下面举一个利用无关项化简的例子。
例2.2.7 要求设计一个逻辑电路,能够判断1位十进制数是奇数还是偶数,当十进制数为奇数时,电路输出为1,当十进制数为偶数时,电路输出为0。
解:第一步,列写真值表。用8421BCD码表示十进制数,4位码即为输入变量,当对应的十进制数为奇数时,函数值为1,反之为0,得到表2.2.4所示的真值表。

注意,8421BCD码只有10个,表中4位二进制码的后6种组合是无关的,1位十进制数不包括10~15,这些无关状态根本不会出现,这后6种变量组合对应的最小项就是无关项,它们对应的函数值可以任意假设,为0为1都可以,通常以×(或O)表示。
第二步,将真值表的内容填人四变量卡诺图,如图2.2.12所示。

第三步 ,画包围圈 ,此时应利用无关项 ,显然 ,将最小项M13、m15、 M11对应 的方格视为1,可以得到最大的包围圈 ,由此可写出L=D.
若不利用无关项 ,L=AD+BCD,结果复杂得多 。
以上讨论的是从一变量到四变量的卡诺图,并以四变量卡诺图为例,分析了逻辑函数的化简方法。至于更多变量,例如五变量或六变量卡诺图的应用,可参阅文献[3]和[4]。



 公网安备44030402000607
公网安备44030402000607





