HLMP-6300-F0021 相位差
发布时间:2019/10/4 23:41:51 访问次数:1290
HLMP-6300-F0021如果将一个正弦电压加到一个电阻上,那么流过电阻上的电流也是正弦波。因为欧姆定律指出电流与电压成正比c图3.1-8在同一时间轴上画出了电流和电压的波形。注意:电压正向增加,电流随之正向增加;电压反向增加,电流也随之反向增加。在所有时间内,电压和电流波形同步变化,因此称这两个波形同相。
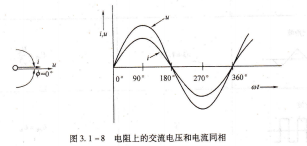
图3,1-8 电阻上的交流电压和电流同相
图3.1-9画出了两个相位不同的电压波形。在起始点0°,“1到达正峰值,电压L2为零。由于这两个波形不是在同一时刻到达最大值和最小值,因此称这两个波形之间存在相位差c该图中两个波形之间的相位差为90°。

图3,1-9 仍I电压超前于扬2电压90°
为了更进一步地描述两个波形之间的相位关系,引人了超前和滞后两个名词。一个波形超前或滞后于另一个波形的大小用角度来衡量。对于图3.1-9所示的两个波形来说,可以这样描述:“2电压滞后于L1电压90°或“j电压超前干I‘2电压90°。相位差一般用Δφ表示,Δφ=φ1-φ2。其中φ1表示・1的初相位,φ2表示“2的初相位。因此,我们可以对Δφ的数值加以讨论:
相位差的取值范围为:0°(Δφ<180°。
当Δφ>0°时,ul电压超前于“2电压;
当Δφ(0°时,IJ 1电压滞后于△2电压;
当Δφ=0°时,乙l电压与己2电压同相;
当Δφ=90°时,%电压与乙2电压正交;如图3.1-9所示。
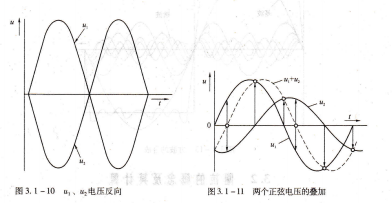
当Δφ=180°时,“1电压与乙2电压反向;如图3.1-10所示。
在电子电路中,“正交”和“反相”两种情况是应用最多的。在后续教材中我们会在具体的电路中加以详细的描述。应当注意,研究两个正弦波的相位差,一般是指两个频率相同的正弦波。因为这样的两个正弦波之间的相位差总是常数。而频率不同的两个正弦波之间的相位差不再是一个常数,它是随时间变化的。因此,研究其相位差的意义不大。
正弦交流电的叠加,当两个或两个以上的正弦波电压加到同一个电路中时,它们之间会产生叠加。其叠加结果与正弦波的频率有关。
两个频率相同的正弦电压相叠加,其波形如图3.1-11所示,从图中可以看到,叠加后
的波形仍然是同频率的正弦波,但其幅度和初相位将发生变化。如果将两个同频率的正弦波相乘,则可以得到一个两倍频率的正弦波,如图3.1-12所示。此外,在曲线上还可以看出正弦波形的斜率变化率,该变化率也是一条正弦曲线。
HLMP-6300-F0021如果将一个正弦电压加到一个电阻上,那么流过电阻上的电流也是正弦波。因为欧姆定律指出电流与电压成正比c图3.1-8在同一时间轴上画出了电流和电压的波形。注意:电压正向增加,电流随之正向增加;电压反向增加,电流也随之反向增加。在所有时间内,电压和电流波形同步变化,因此称这两个波形同相。

图3,1-8 电阻上的交流电压和电流同相
图3.1-9画出了两个相位不同的电压波形。在起始点0°,“1到达正峰值,电压L2为零。由于这两个波形不是在同一时刻到达最大值和最小值,因此称这两个波形之间存在相位差c该图中两个波形之间的相位差为90°。

图3,1-9 仍I电压超前于扬2电压90°
为了更进一步地描述两个波形之间的相位关系,引人了超前和滞后两个名词。一个波形超前或滞后于另一个波形的大小用角度来衡量。对于图3.1-9所示的两个波形来说,可以这样描述:“2电压滞后于L1电压90°或“j电压超前干I‘2电压90°。相位差一般用Δφ表示,Δφ=φ1-φ2。其中φ1表示・1的初相位,φ2表示“2的初相位。因此,我们可以对Δφ的数值加以讨论:
相位差的取值范围为:0°(Δφ<180°。
当Δφ>0°时,ul电压超前于“2电压;
当Δφ(0°时,IJ 1电压滞后于△2电压;
当Δφ=0°时,乙l电压与己2电压同相;
当Δφ=90°时,%电压与乙2电压正交;如图3.1-9所示。
当Δφ=180°时,“1电压与乙2电压反向;如图3.1-10所示。
在电子电路中,“正交”和“反相”两种情况是应用最多的。在后续教材中我们会在具体的电路中加以详细的描述。应当注意,研究两个正弦波的相位差,一般是指两个频率相同的正弦波。因为这样的两个正弦波之间的相位差总是常数。而频率不同的两个正弦波之间的相位差不再是一个常数,它是随时间变化的。因此,研究其相位差的意义不大。
正弦交流电的叠加,当两个或两个以上的正弦波电压加到同一个电路中时,它们之间会产生叠加。其叠加结果与正弦波的频率有关。
两个频率相同的正弦电压相叠加,其波形如图3.1-11所示,从图中可以看到,叠加后
的波形仍然是同频率的正弦波,但其幅度和初相位将发生变化。如果将两个同频率的正弦波相乘,则可以得到一个两倍频率的正弦波,如图3.1-12所示。此外,在曲线上还可以看出正弦波形的斜率变化率,该变化率也是一条正弦曲线。




 公网安备44030402000607
公网安备44030402000607





